プログラミング演習1


― 課題4 数値解析法 ―

【資料】

数値積分-2(pdf)
3.2 シンプソンの公式

シンプソンの公式の1区間分の近似式は
　　I　= 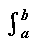int_ab f (x) dx ≒ (h/3)[f (a) + 4f (a +h) + f (b)], h = (b -a) / 2
また、積分範囲を n 分割したときの複合公式は
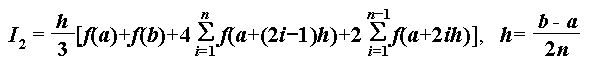
simp_eq
となる。

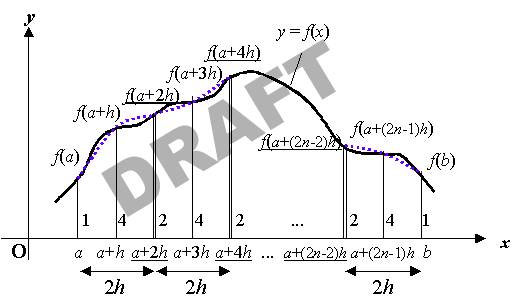
simpson2
シンプソンの公式（複合公式）の基本部分のPADは、たとえば
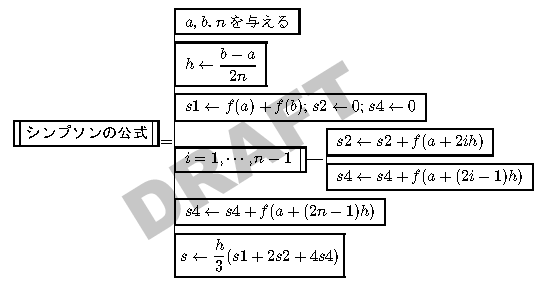
simp_pad2
となる。

台形公式とシンプソンの公式において、計算誤差が分割数の増加とともに減少する 速度を比較するためのプログラムを作成したい。 仕様は以下のとおり。
  1. 台形公式、シンプソンの公式 を用いた数値積分ルーチンを それぞれ独立した倍精度関数 Trapez(), Simpson() として実現する。 引数は積分の下限a , 上限b , 被積分関数f (x) , 分割数n とし、積分の近似値を戻り値で返す。
  2. 2つの公式について、分割数n = 2〜100 に対する 積分の近似値と 理論値の誤差の絶対値 |(理論値) - I | を出力する。 ただし、シンプソンの公式の分割数は内部で(台形公式の)2倍になっているので、 分割数を偶数で増加させ、(台形公式の)半分にして比較することにする。
  3. 被積分関数は f (x) = 4 / (1 + x 2)、 積分範囲は0〜1 とする。（このとき、積分の理論値はπとなる。）
以下のプログラム例は、上記の仕様を満たそうと書きはじめたものである。 ただし、未完成である。 
/*
    simp_tra.c
 */
#include <stdio.h>
#include <math.h>
const double PI=3.14159265358979323846;

double f(double x)
{
    return 4.0 / (1 + x * x);  //  f(x) = 4/(1+x2)
}

double Trapez(double a, double b, double (*f)(double), int n)
/*
    数値積分ルーチン（台形公式）
 */
{
    int i;
    double h, s;

    h = (b - a) / n;
    s = (f(a) + f(b)) / 2;
    for (i = 1; i < n; i++) s += f(a + i * h);
    return h * s;
}

double Simpson(double a, double b, double (*f)(double), int n)
/*
    数値積分ルーチン（シンプソンの公式）
 */
{
    int i;
    double h, s, s2, s4;

    h = ……;
    s = ……;
    s2 = s4 = ……;
    for (i = 1; i < n; i++) {
        s2 += ……;
        s4 += ……;
    }
    s4 += ……;
    s  += ……;
    return ……;
}

int main(void)
{
    int n;
    double a, b;

    a = 0; b = 1;
    printf("# 分割数, 台形公式, シンプソンの公式\n");
    for (n = 2; n <= 100; n += 2) {
        printf("%5d, % .15e, % .15e\n", n, ……, ……);
    }
    return 0;
}
// end of simp_tra.c

出力結果をグラフにした例を以下に示す。

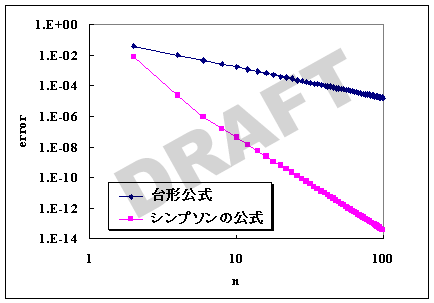
simp_err2

Excelで表示しているグラフの縦軸を対数表示にするには、 縦軸の目盛数字をダブルクリックして「軸の書式設定」メニューを呼び出し、 「目盛」タブにおいて[対数目盛を表示する]をチェックする。 横軸についても同様に行えば両対数グラフになる。

3.3 台形公式による二重積分

ニ重積分の式
　　I = 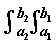int2_ab f (x, y)dxdy
は
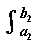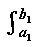　　I = int_ab2 Ix (y) dy , 　　Ix (y) = int_ab1 f (x, y) dx
と書くことにより、2段階の一重積分で表すことができる。

台形公式による二重積分を行い、総分割数(n2)とともに 誤差が減少する様子をみるためのプログラムを作成したい。 仕様は以下のとおり。
  1. 一重積分、二重積分のルーチンをそれぞれ独立した倍精度関数 Trapez1D(), Trapez2D() として実現する。 Trapez1Dの引数は積分の下限a , 上限b , 被積分関数f (x, y) , 変数y, 分割数n とし、積分の近似値を戻り値で返す。 Trapez2D の引数は積分の下限a1, a2 , 上限b1 , b2 , 非積分関数f (x, y) , 分割数n1, n2 とし、積分の近似値を戻り値で返す。
  2. 分割数 n1 = n2 = 1 〜 100 の 2 乗（総分割数）に対する 近似値 I および近似値と理論値との 誤差の絶対値 |(e - 1)2 - I | を出力する。
  3. 被積分関数は f (x, y) = exp(x+y)、 積分範囲はx, y ともに 0〜1 とする。 （このとき、積分の理論値は (e - 1)2 となる。）
以下のプログラム例は、上記の仕様を満たそうと書きはじめたものである。 ただし、未完成である。 
/*
    trapez2d.c: 2重積分(台形公式)
    ∫01∫01 exp(x+y) dx dy
 */
#include <stdio.h>
#include <math.h>

double f(double x, double y)
{
    return exp(x + y);  //  f(x) = exp(x+y)
}

double Trapez1D(double a, double b, double (*f)(double, double), double y, int n)
/*
    積分ルーチン(台形公式): Ix(y) = ∫a1b1 f(x,y) dx
 */
{
    int i;
    double h, s;

    h = (b - a) / n;
    s = (f(a, y) + f(b, y)) / 2;
    for (i = 1; i < n; i++) s += f(a + i * h, y);
    return h * s;
}

double Trapez2D(double a1, double b1, double a2, double b2, double (*f)(double, double), int n1, int n2)
/*
    2重積分ルーチン(台形公式): I = ∫a2b2 Ix(y) dy
 */
{
    int i;
    double h2, s2;

    h2 = ……;
    s2 = ……;
    for (i = 1; i < n2; i++) s2 += ……;
    return ……;
}

int main(void)
{
    int n;
    double a1, a2, b1, b2, s0, s;

    a1 = a2 = 0; b1 = b2 = 1;
    s0 = exp(1)-1; s0 *= s0; // s0 = (e - 1)2
    printf("# 分割数, 二重積分値, 誤差\n");
    for (n = 1; n <= 100; n++) {
        s = Trapez2D(a1, b1, a2, b2, f, n, n);
        printf("%5d, % .15e, % .15e\n", n*n, s, ……);
    }
    return 0;
}
// end of trapez2d.c
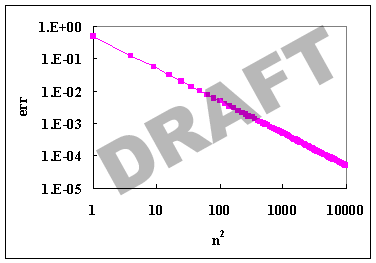
実行結果の誤差のグラフを両対数で描くと以下のようになる。

trapez2_err2

＜＜＜オプション課題＞＞＞

上記2つの未完成プログラム(simp_tra.c, trapez2d.c)のうち、 どちらか一方を完成させ、実行結果から誤差のグラフを両対数で描画し報告せよ。 実行結果については、最初の数行と最後の数行のみを報告し、途中は省略せよ。

余力のある人は、二重積分のプログラムにおいて、(a1, a2), (b1, b2), (n1, n2), (x, y) をそれぞれ配列にしてまとめ、再帰的な定義を用いるなどして m 重積分のルーチンを完成させてみよ。

【目次】 | 【1.】 | 【2.】 | 【3.のトップ】 | 【付録1】 | 【付録2】 【付録3】