プログラミング演習1
― 課題4 数値解析法 ―
2. 非線形方程式
【資料】
非線形方程式-1(pdf)| 2.1 二分法 |
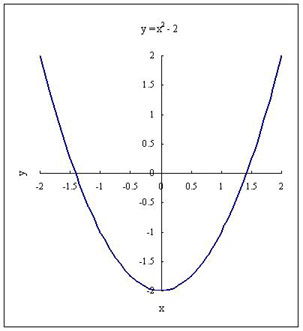
y = f (x) = x 2 - 2 のグラフにおいて、 x 軸との交点を求めれば 2 の平方根 √2 を求めることができる。
 |
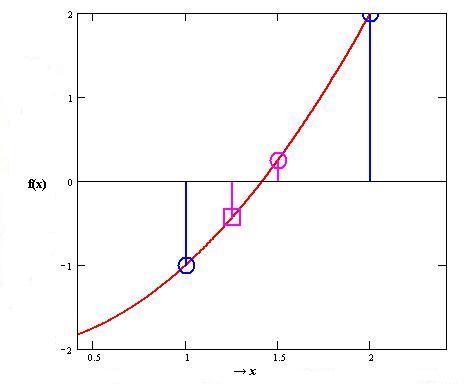 |
√2 は区間 [1, 2] に含まれているが、この区間を中点 x3 = 1.5 で半分ずつに分け、 交点を含む側を選択すると、新しい区間は[1,1.5]となる。 この操作を繰り返すことによって区間 [x1, x2] を順次狭めていき、 交点の近似値を求める方法を 二分法 という。 交点を含む側の選択法は、 x > 0 で y = f (x) が右上がりであることを利用し、 中点での関数値 f (x3) > 0 のときに中点 x3 を 新しい区間の右端とし、そうでないときは x3 を区間の左端とする。
櫻井・熊谷「Pascalで学ぶプログラミング」の例題3.1に記載されている二分法のPADを以下に示す。
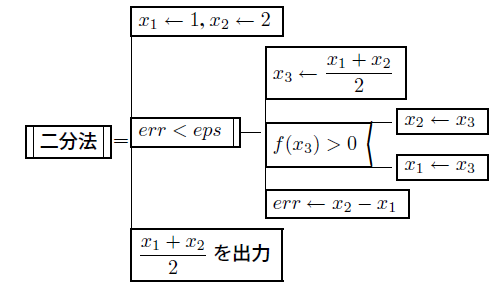
ここに、f (x) = x 2-2 であり、 eps は例えば eps = 1 x 10-6とする。
これをCに移植し、途中経過も出力するように(下線部分を追加)したもの (bisec0.c)を以下に示す。 ただし、アルゴリズムの核心部分は穴埋めする必要がある。
1: /*
2: bisec.c
3: */
4: #include <stdio.h>
5:
6: double f(double x)
7: // f(x) = x^2 - 2
8: {
9: return _____?_____;
10: }
11:
12: int main(void)
13: {
14: int n = 0;
15: double x1, x2, x3, err;
16: double eps = 1.0e-6;
17:
18: x1 = _?_;
19: x2 = _?_;
20: printf("# n, x, err\n");
21: do {
22: n++;
23: x3 = ______?________;
24: if ( ____?____ ) ___?___;
25: else ___?___;
26: err = ___?___;
27: printf("%4d, % .15e, % .15e\n", n, x3, err);
28: } while (____?_____);
29: printf("\n# sqrt(2) = % .15e\n", _______?_______);
30: return (0);
31: }
実行結果が表示されたら、そのウィンドウ(コマンドプロンプト)を右クリックして
「範囲指定(K)」を選択し、コピーする範囲をマウスでドラッグ選択しておき
(選択部分は反転)、[Enter]キーを押す。
これにより選択領域がバッファメモリに一時保存される。
メモ帳、ワードパッド、Word 2003などを開いておいて「貼り付け」を行うと
マウスで選択した実行結果のデータが貼り付けられる。
「名前をつけて保存」によりいったんtxt形式で演習用のフォルダ
(例えばZ:\proen1\kadai4)に保存し、エクスプローラーなどで拡張子を
‘.csv’に変えておく。
「コマンドプロンプト」を使う場合は、bisec.exeファイルがあるところ (例えばZ:\proen1\kadai4\bisec\Debug)まで cd コマンドなどで移動し、
Z:\proen1\kadai4\bisec\Debug>bisec > bisec.csv
とコマンドを実行すると、リダイレクトによりCSVファイル に出力される。
bisec.csv を Excelで呼び出し、グラフに描画したものを以下に示す。
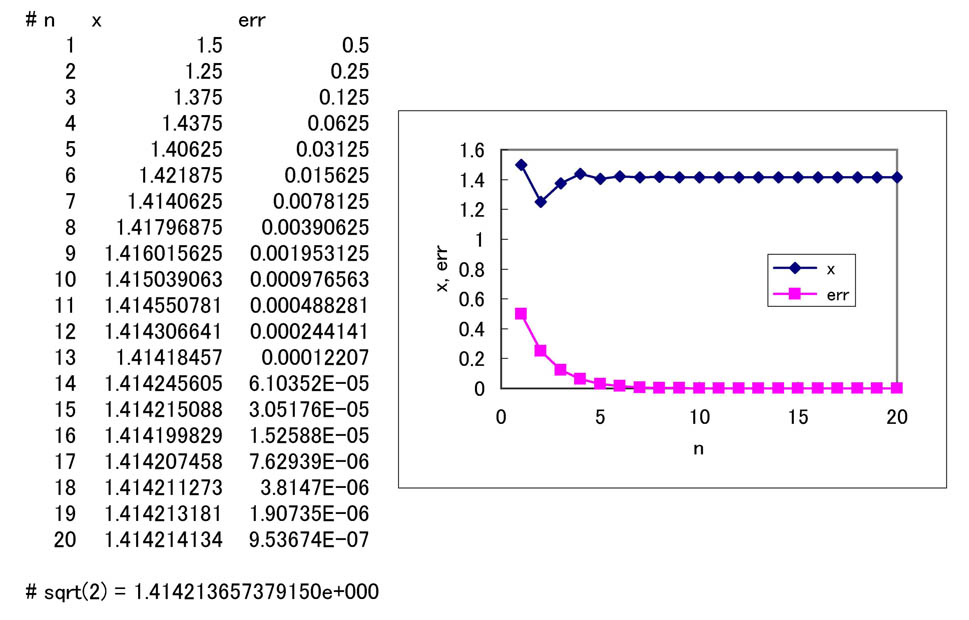
宿題4-1
以下の要求を満たす2分法のプログラムを作成せよ。
【1】 上述のプログラムは精度を自由に変えることができない。
また、もう一つの解 -√2 を求めることも出来ない。
そこで、
[1-1] 初期区間 [x1, x2]
の値と精度eps を入力できること
[1-2] 負の領域の解も求められること
という仕様を追加する。
x < 0 では関数が右下がりになるので、区間を選択する条件が変わる。
if 文を用いて条件を切り替える方法もあるが、
たとえば f (x1)*f (x3)
の符号で判断すれば、余計な場合分けをしなくて済む。
→ 動作テストとして、初期区間 [-2, -1], eps = 1e-10
の場合を実行してみよ。
【2】 初期区間を入力するようにしたプログラムでは、
誤差を極端に小さくした場合(たとえば eps = 1e-16 )に
do〜while の反復が止まらなくなる。
また、交点が0かまたは2個以上あるような区間から開始した場合
(たとえば[2, 6], [-6, -2], [-2, 6], [-6, 2]など)や、
x1, x2 の大きさが
x1 > x2 の場合、
誤った結果を求めてしまう。
そこで、
[2-1] 反復が止まらない場合はエラーメッセージ
“*** 反復回数が100回を超えました。***” を表示して
有限回(N = 100)で止まること
[2-2] 入力値が x1 > x2
でも解が求められること
[2-3] 初期区間の数値が異常な場合
(例えばf (x3)とf (x1),
f (x2)の符号がすべて同じ場合)
は入力エラーメッセージ“*** 初期区間の数値が異常です。***”
を表示して終了すること
という仕様を追加する。
→ 動作テストとして eps = 1e-16 とした場合、x1 = 2,
x2 = 1 とした場合、
[x1, x2] = [2, 6], [-6, -2], [-2, 6], [-6, 2]
とした場合の対策後の動作を検証してみよ。
【3】 さらに余力のある人は、上記の機能を保ったまま、以下の要求を満たしてみよ。
[3-1] 二分法のアルゴリズムの部分(bisec.cの20行め〜28行めに相当する部分)
を bisection() と名づけ、
main関数から独立させる。
double bisection(double x1, double x2, double eps)
{
…………………………
二分法のアルゴリズム
…………………………
return (x1 + x2) / 2.0;
}
[3-2] 方程式の左辺の関数 f (x) の名前をmain関数側で
自由に指定できるように bisection の引数に関数引数用の
定義(関数ポインタ)を追加する。
double bisection(double (*f)(double), double x1, double x2, double eps)
{
…………………………
二分法のアルゴリズム
…………………………
return (x1 + x2) / 2.0;
}
【目次】 | 【1.】 | 【2.のつづき】 | 【3.】 | 【付録1】 | 【付録2】 | 【付録3】