プログラミング演習1


― 課題4の付録3 ―

【資料】

課題4の付録3(pdf)

ニュートン・コーツの公式の打切り誤差

→ 川上一郎 「数値計算」 第5章 5.1 (pp.123〜124) 参照

「ニュートン・コーツの公式」は、1次式近似の「台形公式」、 2次式近似の「シンプソンの公式」を一般化し、 f(x) を n次多項式で近似したときの 積分公式である。

「ニュートン・コーツの公式」の打切り誤差は、n が奇数のとき
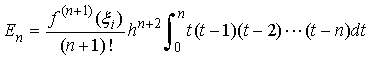
　　　En_odd
n が偶数のとき
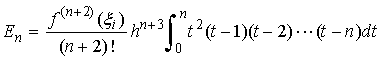
　　　En_even
である。ここに、ξi は、x = xi から xi+n までの小区間のなかのある x の値 xi < ξ < xi+n である。

「台形公式」(n = 1)の場合
　　　E1
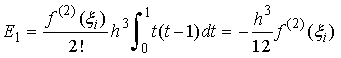
「シンプソンの公式」(n = 2)の場合
　　　E2

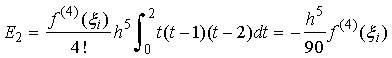
n が大きいほど打切り誤差は小さくなる傾向があるが、 n が偶数のときのほうが奇数のときよりも有利である。

【目次】 | 【1.】 | 【2.】 | 【3.】 | 【付録1】｜ 【付録2】