プログラミング演習1


― 課題4 数値解析法 ―

【資料】

非線形方程式-2(pdf)

【数値解析補助資料】

数値解析の講義スライド一部抜粋（非線型方程式）
参考：数値計算入門「河村哲也著」第2章・非線形方程式その1
2.2 ニュートン法

ニュートン法は以下の手順で方程式 f (x)=0 の解を求める。

  1. 初期値x0を与える。
  2. その点での関数値f (x0)と 傾きf '(x0)から x 切片x1を推定する。
  3. x1を新たな初期値x0としてこの操作を反復する。
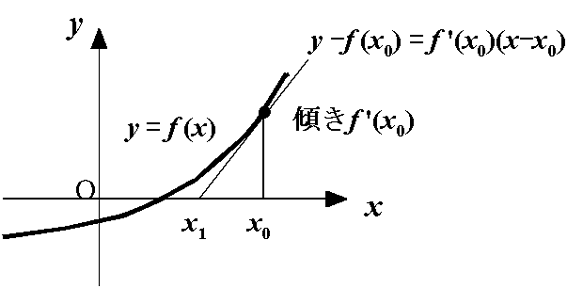
newton

(x0, f (x0))を通る接線の式
　　y - f (x0) = f '(x0) (x - x0)
においてx 切片では y = 0, x = x1 となるので
　　x1 = x0 - f (x0) / f '(x0)　　　　　　　　　　　　　　　……… (2.1)
f (x) = x2 - a のとき、f '(x) = 2x だから
　　x1 = x0 - (x02 - a) / 2x0 = (x0 + a / x0) / 2 　　……… (2.2)

真野芳久「Pascalプログラミングの基礎」サイエンス社 p.41 のプログラムと 川上一郎「数値計算」岩波書店 p.180 付録3.1のプログラムを合体してCに移植し、 手直ししたもの(newton0.c)を以下に示す。 ただし、アルゴリズムの核心部分は穴埋めする必要がある。
下線部では scanf関数の代わりにfgets関数とsscanf関数 を使って入力する方法を用いた。→[付録1]
また、リダイレクト出力時にも入力促進メッセージ等がコマンドプロンプトに 出力されるようにfprintf関数を用いて 標準エラー出力(stderr)とした。 

 1: /*
 2:     newton.c: ニュートン法
 3:  */
 4: #include <stdio.h> // printf, fgets, sscanf
 5: #include <math.h>  // fabs
 6:
 7: int main(void)
 8: {
 9:     int n = 0;
10:     double a = 2, x, x0, err, eps = 1.0e-10;
11:     char s[128];
12:
13:     fprintf(stderr, " a = "); fgets(s, 128, stdin); sscanf(s, "%lf", &a);
14:     while (a <= 0.0) {
15:         fprintf(stderr, "'a' には正の数を入れてください。\n");
16:         fprintf(stderr, " a = "); fgets(s, 128, stdin); sscanf(s, "%lf", &a);
17:     }
18:
19:     x = (a + 1.0) / 2.0;
20:     printf("# n, x, err\n");
21:     printf("%4d, % .15e\n", n, x);
22:     do {
23:         n++;
24:         x0 = _;
25:         x = _______?_______;
26:         err = _____?_____;
27:         printf("%4d, % .15e, % .15e\n", n, x, err);
28:     } while (_____?_____);
29:     printf("\n# sqrt(%e) =  % .15e\n", a, x);
30:     return 0;
31: }

主要部分のアルゴリズムをPADで描くと

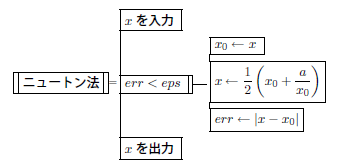
newtn_pad

" a = 2" を入力したときの実行結果とそのグラフは

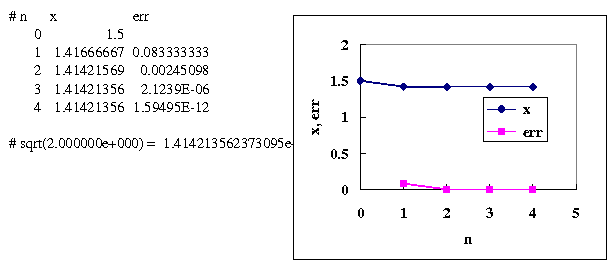
newton1

2.3 二元連立非線形方程式（ニュートン法）

n 元連立非線形方程式は一般に
　　f1(x1, x2, ..., xn) = 0,
　　f2(x1, x2, ..., xn) = 0,
　　　...　...　...　...　...
　　fn(x1, x2, ..., xn) = 0
と書くことができる。これをベクトル表記すると
　　f (x) = 0
となる。

このとき、ニュートン法の計算式は
　　xk+1 = xk + u (xk)
　　　　　 = xk - J (xk)-1 f (xk)
となる。ここに、 J (xk) はヤコビ行列と呼ばれ、
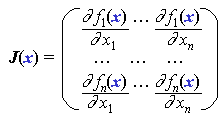
　　jacobian
であり、また、 u (x) = - J (x)-1 f (x) である。

2変数の場合は、逆行列が簡単に求められるので
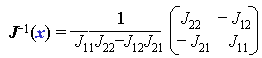
　　jacobian2_
ここに
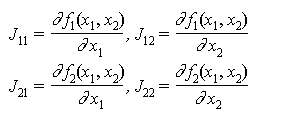
　　jacobian2

「数値解析」の講義用にWebページで公開してある 「連立非線形方程式」を解くプログラム(Newton2.c)を 一部手直ししたものを以下に示す(newton2.c)。 このプログラムは
　　x 2 + y 2 = 1, 　　　 y = x 3
を解くためのものである。仕様は以下のとおり。
  1. 入力は初期値(x0, y0)のみ。許容誤差は eps = 10-10。
  2. 出力は途中経過と最終結果。CSV形式に対応。
  3. 方程式の左辺の関数2つはおのおの独立に定義。（結果は戻り値で返す。）
  4. ヤコビ行列の4つの要素もおのおの独立に定義。（結果は戻り値で返す。）
  5. 補正ベクトルu (x)計算ルーチンの結果は2つの引数で返す。
  6. 2変数ニュートン法ルーチンの計算結果は2つの引数で返す。 
 1: /*
 2:     newton2.c: 2変数のニュートン法
 3:     x2+y2=1, y=x3 -> (x,y)=(0.826,0.5636),(-0.826,-0.5636)
 4:  */
 5: #include <stdio.h> // printf, fprintf, fgets, sscanf
 6: #include <math.h>  // hypot(hypotenuse): 直角三角形の斜辺を求める関数
 7:
 8: double f1(double x, double y)
 9: {
10:     return x * x + y * y - 1; //  f1(x,y) = x2 + y2 - 1
11: }
12: double f2(double x, double y)
13: {
14:     return x * x * x - y;     //  f2(x,y) = x3 - y
15: }
16: 
17: double J11(double x, double y)
18: {
19:     return 2 * x;     //  df1(x,y)/dx = 2x
20: }
21: double J12(double x, double y)
22: {
23:     return 2 * y;     //  df1(x,y)/dy = 2y
24: }
25: double J21(double x, double y)
26: {
27:     return 3 * x * x; //  df2(x,y)/dx = 3x2
28: }
29: double J22(double x, double y)
30: {
31:     return -1;        //  df2(x,y)/dy = -1
32: }
33: 
34: int ucalc(double x, double y, double *ux, double *uy)
35: /*
36:     u = -J-1(x)*f(x)
37:  */
38: {
39:     double det;
40: 
41:     det = J11(x, y) * J22(x, y) - J12(x, y) * J21(x, y);
42:     *ux = -1 / det * (J22(x, y) * f1(x, y) - J12(x, y) * f2(x, y));
43:     *uy =  1 / det * (J21(x, y) * f1(x, y) - J11(x, y) * f2(x, y));
44:     return 0;
45: }
46: 
47: int newton2(double *x, double *y, double eps)
48: {
49:     int n=0;
50:     double x0, y0, ux, uy, err;
51: 
52:     printf("# n, x, y, err\n");
53:     printf("%4d, % .15e, % .15e\n", n, *x, *y);
54:     do {
55:         n++;
56:         x0 = *x; y0 = *y;
57:         ucalc(*x, *y, &ux, &uy);
58:         *x += ux; *y += uy;        // xk+1 = xk + u(xk)
59:         err = hypot(*x - x0, *y - y0);
60:         printf("%4d, % .15e, % .15e, % .15e\n", n, *x, *y, err);
61:     } while (err >= eps);
62:     return 0;
63: }
64: //  ------------    Main    ------------
65: int main(void)
66: {
67:     double x=1, y=0.5, eps = 1e-10;
68:     char s[128];
69:
70:     fprintf(stderr, "# x0 y0 = "); fgets(s, 128, stdin); sscanf(s, "%lf%lf", &x, &y);
71:     newton2(&x, &y, eps);
72:     printf("\n# (x y) = (% .15e % .15e)\n", x, y);
74:     return 0;
75: }

"# x0 y0 = 1　0.5" と入力したときの実行結果とグラフは
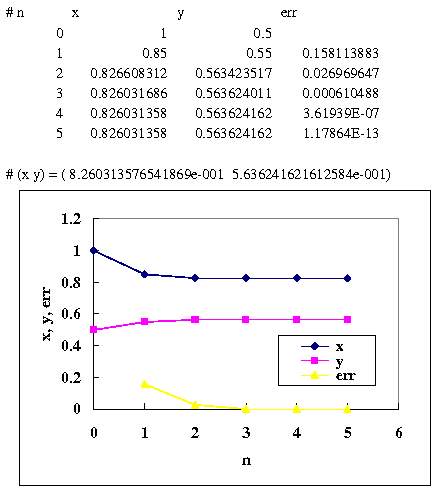
newton2

　

＜＜＜レポート課題4（※6月30日一部変更）＞＞＞

上記2つのプログラムを以下の要求に沿って改良せよ。なお、【1】をレポート課題として、【2】はオプション課題とする。

【1】 2.2 のニュートン法のプログラム newton.c では、f (x ) = x2-a を仮定した後、手計算した式(2.2)を使っているので、 2.1 の二分法や 2.3 の連立非線形方程式のプログラムのように 方程式の左辺の関数が独立していない。 そこで、以下の要求を満たすプログラムを作成せよ。
【1-1】 式(2.1)を用い、方程式の左辺関数 f (x) (= x 2 - a ) および その導関数 f '(x) を独立させる。 ただし、入力変数 a はグローバル変数としてよい。 導関数 f '(x) は、プログラムでは例えばdf (x) と名づけておく。

【1-2】 ニュートン法のアルゴリズムの部分 (newton.c の 20行目〜28行目)を newton() と名づけ、 main関数から独立させる。

double newton(double x, double eps)
{
    …………………………………
    ニュートン法のアルゴリズム
    …………………………………
    return x;
}
【1-3】 方程式の左辺の関数 f (x) と その導関数の名前をmain関数側で自由に指定できるように、 newton() の引数に関数引数用の定義(関数ポインタ)を追加する。 
double newton(double x, double (*f)(double), double (*df)(double), double eps)
{
    …………………………………
    ニュートン法のアルゴリズム
    …………………………………
    return x;
}

【1-4】 a の数値をコマンド行から入力する。

なお、実行例として a = 3 および 5 の場合について報告せよ。

【2】 2.3 の2変数のニュートン法のプログラム newton2.c は、 同じような関数が多くてソースが冗長である。 そこで、以下の要求を満たすプログラムを作成せよ。
【2-1】 関数f1(), f2()を配列 f[1], f[2]、 関数J11()〜J22()を2次元配列 J[1][1]〜J[2][2] に割り当てることにして、 方程式の左辺関数f (x)と そのヤコビ行列 J (x)を おのおの一つのサブルーチン(func(), Jcalc())にまとめること。
ただし、関数の戻り値で渡していた値は引数で受け渡すことにし、 手続きの戻り値は終了コード(整数)とする。 

int func(double x, double y, double f[])
{
    ……………………
    f[1] = …………;
    f[2] = …………;
    return 0;
}
また、Cでの配列の定義は0から始まることに注意し、一つ多めに宣言しておく。 配列の数(ND)をヘッダのインクルードの下で以下のように定数マクロで宣言しておくとよい。
#define ND 3

2次元配列を引数でうまく渡せなかった人は、 次善の策として1次元配列にして渡すか、大域変数で引き渡すこと。

【2-2】 変数x, yを配列x[1], x[2]、 変数ux, uyをu[1], u[2]に割り当てて サブルーチン等の引数の数を減らし、n 変数に移行しやすくする。

【2-3】 方程式の左辺の関数 f (x) と その導関数の名前をmain関数側で自由に指定できるように、 newton2() の引数に関数引数用の定義(関数ポインタ)を追加する。

なお、実行例として
　　x 2 + (y/2)2 = 1, 　　y 2 = x 2 + 1
について、第1象限の解を求めてみよ。

【目次】 | 【1.】 | 【2.のトップ】 | 【3.】 | 【付録1】 【付録2】