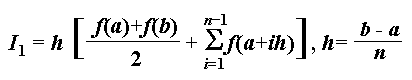プログラミング演習1

― 課題4 数値解析 ―

3. 数値積分

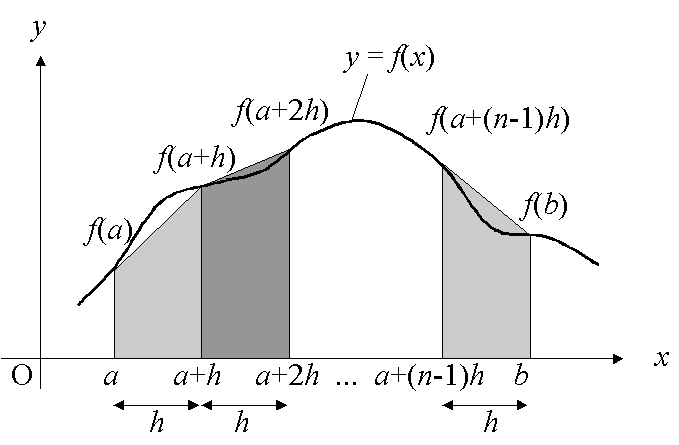
3.1 台形公式

台形公式の1区間分の近似式は
　　I = ∫_a^b f (x ) dx ≒ (b -a )[f (a ) + f (b )] / 2
積分範囲を n 分割したときの複合公式は
　　

この式からPADを素直に描くと以下のようになる。

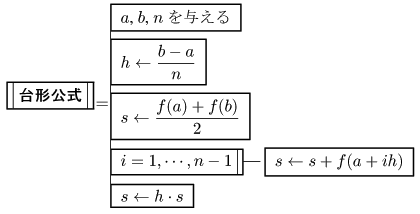
ここで、f (a +ih)のカッコ内の乗算をなくすために x_i = a +ih とおき、
　　x ₀ = a,　　x_i +1 = x_i +h
というように帰納的に計算すると、以下のようになる。

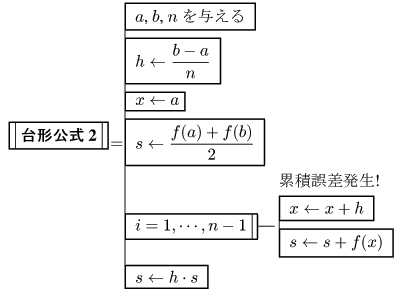
しかし、このアルゴリズムでは加算による丸め誤差の累積が発生しやすい。 実際、台形公式による積分計算を単精度(float)で行うプログラムを用いて、 上記2つのアルゴリズムを比較してみる。

 1: #include <stdio.h>
 2: #include <math.h>
 3:
 4: float f(float x)
 5: {
 6:     return 4.0 / (1 + x * x);  //  f(x) = 4/(1+x2)
 7: }
 8:
 9: float Trapez(float a, float b, float (*f)(float), int n)
10: /*
11:  *  累積誤差がない単精度の数値積分ルーチン（台形公式）
12:  */
13: {
14:     int i;
15:     float h, s;
16:
17:     h = (b - a) / n;
18:     s = ((*f)(a) + (*f)(b)) / 2;
19:     for (i = 1; i < n; i++) {
20:         s += (*f)(a + i * h); // 累積誤差はない
21:     }
22:     return h * s;
23: }
24:
25: float Trapez2(float a, float b, float (*f)(float), int n)
26: /*
27:  *  累積誤差がある単精度の数値積分ルーチン（台形公式）
28:  */
29: {
30:     int i;
31:     float h, x, s;
32: 
33:     h = (b - a) / n;
34:     x = a;
35:     s = ((*f)(a) + (*f)(b)) / 2;
36:     for (i = 1; i < n; i++) {
37:         x += h;               // 累積誤差発生要因
38:         s += (*f)(x);
39:     }
40:     return h * s;
41: }
42:
43: main()
44: {
45:     int n;
46:     float a, b, s;
47:
48:     a = 0; b = 1;
49:     printf("# 分割数, 累積誤差なし, 累積誤差あり\n");
50:     for (n = 40; n <= 10000; n += 20)
51:         printf("%5d, % .15e, % .15e\n", n, Trapez(a, b, f, n), Trapez2(a, b, f, n));
52:     return 0;
53: }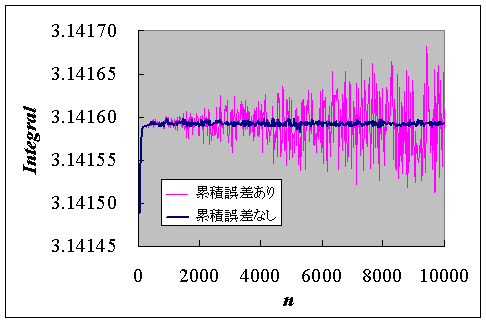

計算結果を示すと以下のようになる。

練習問題

(1) 上記の結果を確認せよ。
(2) 倍精度(double)で計算し、単精度の結果と比較してみよ。

---

【目次】 | 【1.】 | 【2.】 | 【3.のつづき】 | 【付録1】 | 【付録2】