プログラミング演習1

― 課題4 数値解析 ―

1. Cによる数値解析のための準備

1.1 数学関数

Cには標準ライブラリの中に数学関数が用意されており、 ヘッダ <math.h> を インクルードすることで使用可能となる。

注： UNIX用のCコンパイラでは数学関数ライブラリのリンクが必要となる。 「undefined reference to `……'」などのリンクエラーが出たときはそれが原因である。

ヘッダ <math.h> 内には使用できる関数が具体的に宣言されている。 Cで使用できる主な数学関数を以下に示す。

sin(x)	三角関数 sin(x) を計算する。
cos(x)	三角関数 cos(x) を計算する。
tan(x)	三角関数 tan(x) を計算する。
asin(x)	逆三角関数 sin-1(x) を計算する。(-π/2〜π/2)
acos(x)	逆三角関数 cos-1(x) を計算する。(0〜π)
atan(x)	逆三角関数 tan-1(x) を計算する。(-π/2〜π/2)
atan2(y,x)	逆三角関数 tan-1(y/x) を計算する。(-π〜π)
sinh(x)	双曲線関数 sinh(x) を計算する。
cosh(x)	双曲線関数 cosh(x) を計算する。
tanh(x)	双曲線関数 tanh(x) を計算する。
exp(x)	指数関数 ex を計算する。
log(x)	自然対数 ln(x) を計算する。(x > 0)
log10(x)	10 を底とする対数 log10(x) を計算する。(x > 0)
pow(x,y)	べき乗 xy を計算する。
sqrt(x)	実数 x の平方根を求める。(x ≥ 0)
ceil(x)	実数 x より小さくない最小の整数を返す。
floor(x)	実数 x より大きくない最大の整数を返す。
fabs(x)	絶対値|x|を求める。
ldexp(x,n)	x・2n を計算する。
frexp(x,&exp)	実数 x を仮数部と指数部(2のべき乗) exp に分解する。
modf(x,&ip)	実数 x を整数部 ip と小数部に分ける。
fmod(x,y)	実数の剰余(x % y に相当)を求める。

VC++のエディタ内でfabs等の関数名にカーソルを合わせ、 [F1]キーを押すとその関数のヘルプページが表示される。 おのおのの関数の詳しい使い方はここで調べることができる。 (ポップアップメニューが現れた場合は「Visual C++プログラマーズガイド」を選択する。) ページの下のほうに「浮動小数点サポートルーチン」へのリンクがある。 左側の[お気に入り]タブに移って[追加]ボタンで登録していくとよい。

練習1 pi.c (円周率を求める)

 1: #include <stdio.h>
 2: //#include <math.h>
 3:
 4: main()
 5: {
 6:     printf("PI = % .20g\n", 4.0*atan(1.0));
 7:     return 0;
 8: }

2行目のコメントをはずさないと、どのようなエラーが出るか確認せよ。
ちなみに、通常は

 #define PI 3.14159265358979323846

をソースの #include の下に貼り付ければ、定数 "PI" に円周率を割り当てたことになる。

1.2 数に関するユーティリティ

ヘッダ<stdlib.h> には、いくつかの有用な数値変換関数が宣言されている。

atof(s)	文字列 s を double型浮動小数点数に変換する。
atoi(s)	文字列 s を int型整数に変換する。
atol(s)	文字列 s を long型整数に変換する。
rand()	0〜RAND_MAXの範囲の整数乱数を発生する。
srand(seed)	rand() の種として seed をセットする。
abs(n)	int型整数 n の絶対値 |n|を返す。
labs(n)	long型整数 n の絶対値 |n|を返す。

練習2 rand10.c (乱数を発生する)

 1: #include <stdio.h>
 2: //#include <stdlib.h>
 3:
 4: main()
 5: {
 6:     int i;
 7:     for (i=0; i<10; i++) printf("%2d: %d\n", i, rand());
 8:     return 0;
 9: }

2行目のコメントをはずさないと、どのようなエラーが出るか確認せよ。
実行のみを繰り返したとき、結果が変わるかどうか確認せよ。

1.3 整数に関する制限

ヘッダ <limits.h> には整数型のサイズを表す定数が定義されている。

CHAR_BIT	char型のビット数
CHAR_MAX	char型の最大値
CHAR_MIN	char型の最小値
INT_MAX	int型の最大値
INT_MIN	int型の最小値
LONG_MAX	long型の最大値
LONG_MIN	long型の最小値
SHRT_MAX	short型の最大値
SHRT_MIN	short型の最小値

UCHAR_MAX	unsigned char型の最大値
UINT_MAX	unsigned int型の最大値
ULONG_MAX	unsigned long型の最大値
USHRT_MAX	unsigned short型の最大値

VC++のエディタ内でINT_MAX等の定数マクロ名にカーソルを合わせ、 [F1]キーを押すと「データ型定数」のヘルプページが現れる。 おのおのの定数の詳しい意味と具体的な数値はここで調べることができる。 [お気に入り]タブに移って[追加]ボタンで登録していくとよい。

練習3 chkint.c (標準的な整数のビットサイズと制限の確認)

 1: #include <stdio.h>
 2: //#include <limits.h>
 3:
 4: main()
 5: {
 6:     printf("int: %u bit, unsigned: %u bit\n", sizeof(int)*8, sizeof(unsigned)*8);
 7:     printf("INT_MAX = % d\n", INT_MAX);
 8:     printf("INT_MIN = % d\n", INT_MIN);
 9:     printf("UINT_MAX = %u\n", UINT_MAX);
10:     return 0;
11: }

2行目のコメントをはずさないと、どのようなエラーが出るか確認せよ。

1.4 浮動小数点数に関する定数

ヘッダ <float.h> には浮動小数点数に関する様々な定数が定義されている。

単精度
_FLT_RADIX	指数表現における基数b
_FLT_ROUNDS	丸めのモード
FLT_DIG	精度の10進けた数
FLT_EPSILON	計算機イプシロン
FLT_MANT_DIG	浮動小数点数の有効数字部（_FLT_RADIXを基数とする）のけた数p
FLT_MAX	表現可能な最大の有限浮動小数点数
FLT_MAX_EXP	表現可能な数の指数の最大値
FLT_MIN	最小の正規化された正の浮動小数点数
FLT_MIN_EXP	最小正規化数の指数の値

倍精度
_DBL_RADIX	指数表現における基数b
_DBL_ROUNDS	丸めのモード
DBL_DIG	精度の10進けた数
DBL_EPSILON	計算機イプシロン
DBL_MANT_DIG	浮動小数点数の有効数字部（_DBL_RADIXを基数とする）のけた数p
DBL_MAX	表現可能な最大の有限浮動小数点数
DBL_MAX_EXP	表現可能な数の指数部の最大値
DBL_MIN	最小の正規化された正の浮動小数点数
DBL_MIN_EXP	最小正規化数の指数部の値

VC++のエディタ内でDBL_MAX等の定数マクロ名にカーソルを合わせ、 F1キーを押すと「データ型定数」のヘルプページが現れる。 おのおのの定数の詳しい意味と具体的な数値はここで調べることができる。 [お気に入り]タブに移って[追加]ボタンで登録していくとよい。

練習4 chkflt.c (浮動小数点数のビットサイズと制限の確認)

 1: #include <stdio.h>
 2: //#include <float.h>
 3:
 4: main()
 5: {
 6:     printf("float: %u bit, double: %u bit\n", sizeof(float)*8, sizeof(double)*8);
 7:     printf("FLT_MAX =     % e\n", FLT_MAX);
 8:     printf("FLT_MIN =     % e\n", FLT_MIN);
 9:     printf("FLT_EPSILON = % e\n", FLT_EPSILON);
10:     printf("DBL_MAX =     % e\n", DBL_MAX);
11:     printf("DBL_MIN =     % e\n", DBL_MIN);
12:     printf("DBL_EPSILON = % e\n", DBL_EPSILON);
13:     return 0;
14: }

2行目のコメントをはずさないと、どのようなエラーが出るか確認せよ。

1.5 関数ポインタ

非線形方程式や数値積分、微分方程式のサブルーチンを作成する場合、 その引数の一つに関数名を指定できるようにすれば、サブルーチンを呼び出す側に 関数名の決定権を譲ることになり、非常に汎用性の高いサブルーチンとなる。 それを実現するために使われるのが関数ポインタである。

例えば後述する「二分法」のサブルーチンで方程式 f (x)=0 の左辺の関数 f (x) を任意の名前で呼び出せるようにするには、 仮の関数名 f に*(アスタリスク)を付けて カッコで閉じた関数名 (*f) を用いて(つまり関数ポインタとして) サブルーチンの引数リスト内に引数をつけて定義しておく。

double bisection(double (*f)(double x), double x1, double x2)
{
    二分法の本体
}

さらに、このサブルーチン内部で関数を呼び出すときは

    if ((*f)(x1) * (*f)(x3) < 0) x2 = x3;

というように引数リスト内で定義したものと同じ形式で呼び出すようにしておく。

方程式の左辺の関数が実際には func1(x) という名前で定義されているなら、 main関数で二分法のサブルーチンを呼び出すときに

    x = bisection(func1, x1, x2);

と実際の関数名を引数なしで指定して呼び出せばよい。

練習5 funcp.c (関数ポインタの使用)

 1: #include <stdio.h>
 2:
 3: double func1(){return 1.0;}
 4:
 5: double func2(){return 2.0;}
 6:
 7: double func_p(double (*f)()){return (*f)();} // 関数ポインタを用いたサブルーチン
 8:
 9: main()
10: {
11:     printf("func1 = % g\n", func_p(func1)); // func1 を指定して func_p を呼び出す
12:     printf("func2 = % g\n", func_p(func2)); // func2 を指定して func_p を呼び出す
13:     return 0;
14: }

1.6 Excelによるグラフ描画

出力データをCSV形式で保存すれば、 Excelでただちに読み出すことができる。 CSV形式は一組のデータを単にコンマで区切り、組ごとに改行すればよい。 ファイル保存で名前をつける際、拡張子を“.csv” とする。 先頭行にデータの名前を入れておくと後で便利である。

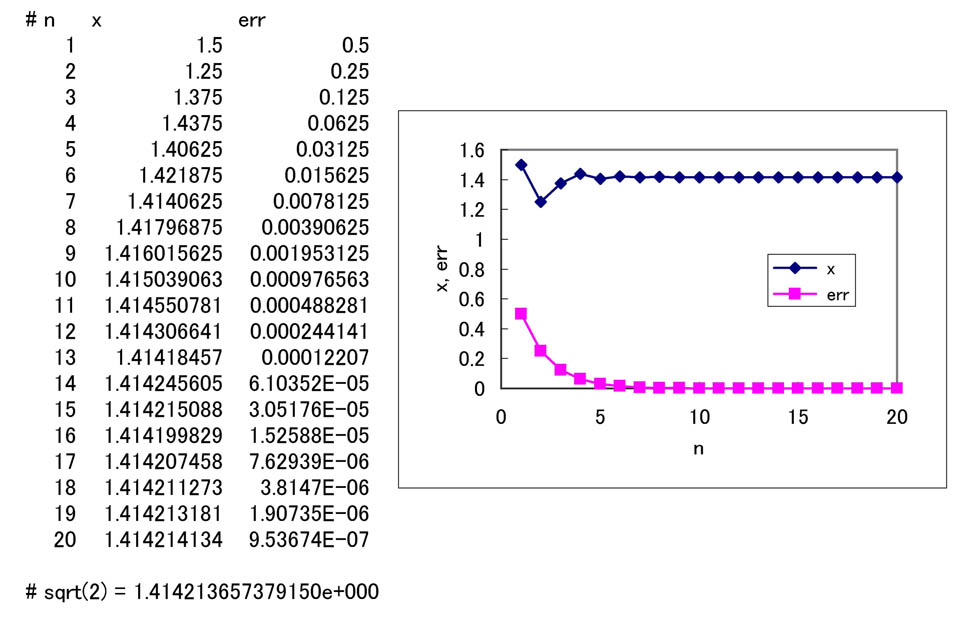
以下の例は後述の2分法の出力ファイルで、名前を“bisection.csv”とする。

---

# n, x, err
   1, 1.500000000000000e+000, 5.000000000000000e-001
   2, 1.250000000000000e+000, 2.500000000000000e-001
   3, 1.375000000000000e+000, 1.250000000000000e-001
   4, 1.437500000000000e+000, 6.250000000000000e-002
   5, 1.406250000000000e+000, 3.125000000000000e-002
   6, 1.421875000000000e+000, 1.562500000000000e-002
   7, 1.414062500000000e+000, 7.812500000000000e-003
   8, 1.417968750000000e+000, 3.906250000000000e-003
   9, 1.416015625000000e+000, 1.953125000000000e-003
  10, 1.415039062500000e+000, 9.765625000000000e-004
  11, 1.414550781250000e+000, 4.882812500000000e-004
  12, 1.414306640625000e+000, 2.441406250000000e-004
  13, 1.414184570312500e+000, 1.220703125000000e-004
  14, 1.414245605468750e+000, 6.103515625000000e-005
  15, 1.414215087890625e+000, 3.051757812500000e-005
  16, 1.414199829101563e+000, 1.525878906250000e-005
  17, 1.414207458496094e+000, 7.629394531250000e-006
  18, 1.414211273193359e+000, 3.814697265625000e-006
  19, 1.414213180541992e+000, 1.907348632812500e-006
  20, 1.414214134216309e+000, 9.536743164062500e-007

# sqrt(2) = 1.414213657379150e+000

---

#(シャープ)記号はGnuPlotで描画するときに コメント行となるようにするためのもので、 Excelでしか描画しないのであればなくてもよい。

1. “bisection.csv”のアイコンをダブルクリックする。
   • ファイル名 *.csv には Excel 2000 が関連付けられているので、 Excel 2000 が起動し、bisection.csv が読み込まれる。
2. グラフを作成するために、データの範囲を選択する。 以下の操作により、データ範囲をすばやく選択できる。
   • セル A1 が選択されていることを確認。
   • Ctrl キーと Shift キーを押しながら → キーを押す。
   • Ctrl キーと Shift キーを押しながら ↓ キーを押す。
   • 数値の範囲が反転し、選択されていることを確認する。
3. グラフウィザードボタン を押す。
4. グラフウィザードダイアログが表示されるので、以下の操作を行う。
   • [グラフの種類(C)] で散布図を選択。
   • [形式(T)] で左下の「データポイントを折れ線でつないだ散布図です。」を選択。
   • [次へ > ] ボタンを2回クリックし、[タイトルとラベル] タブの X/数値軸(A) に "n" を、 Y/数値軸(V) に "x, err" を記入する。
   • [目盛線] タブを選択し、Y/数値軸の目盛線(O) のチェックをはずす。
   • [完了(F)] ボタンをクリック。
5. 好みに応じて軸の目盛の範囲や凡例の位置、背景などを変更する。

   グラフをコピーして Word 2000 など他のアプリケーションに貼り付けることも可能である。

   

練習6 (Excelによるグラフの描画)

• まず“bisection.csv”を右クリックし、 「対象をファイルに保存」で演習1課題4用のフォルダ(例えばZ:\enshu1\kadai4)に保存する。
• 実際に上記の操作を行い、グラフを描いてみよ。

1.7 GnuPlotによるグラフ描画

GnuPlotは、"sister"の public(P:) の 伊藤/演習1数値解析/wgpl+w32/wgnplot.exe から起動できる。

1. 起動した後、[ファイル]→[ディレクトリの移動]で カレントディレクトリを、例えば "Z:\enshu1\kadai4" など、 CSVファイルがあるディレクトリ(フォルダに相当)に変える。
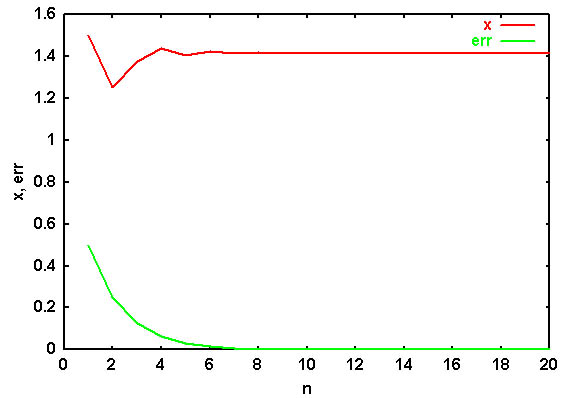
2. plot　"bisection.csv"　t　"x"　w　l, 　"bisection.csv"　u　1:3　t　"err"　w　l と入力する。
3. 別ウィンドウにグラフが描画される。
4. set　xlabel　"n" と入力する。
5. set　ylabel　"x, err" と入力する。
6. replot と入力する。rep のみでもよい。
7. グラフ内で右クリックし、好みに応じてフォント(Font)や線種(Line Style)を変更する。

   グラフ内で右クリックし、"Copy to Clipboard" を選択すれば、他のアプリケーションに貼り付けることができる。

   

詳しくは GnuPlot日本語マニュアル を参照のこと。

1.8 PADについて

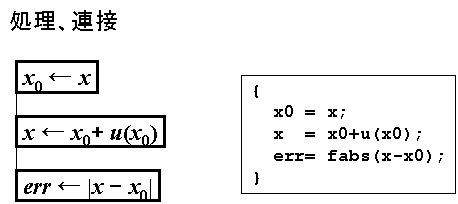
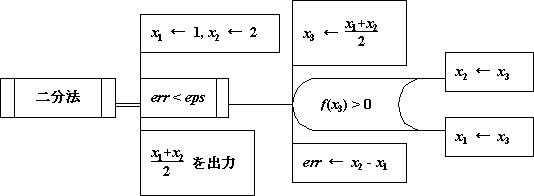
PADとはProblem Analysis Diagramの略である。 構造化フローチャートの一種で、処理の方向は「上から下へ」流れる。 具体的な処理内容が書かれた「処理箱」と呼ばれる 横長の四角い箱の左端を「縦線で結合(連接)」することによりプログラムのフローをあらわす。 Cにおいては、処理箱は文に、連結されたものはブロックに相当する。

「判断(選択)」、「反復」などの処理の中の文・ブロックはそれらの箱の右側に置き、横線で結ぶ。 これらの処理ではフローをいったん右側の文・ブロックに移す。 ブロックの場合は上からはじまり、一番下で左側に戻る。
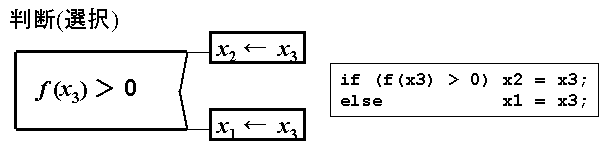
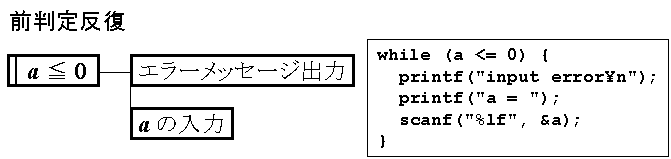
「判断(if文)」は、箱の右辺が中折れしており、 上下の頂点から横に１本ずつ2本の分岐線を伸ばすことができ、 条件によっていずれか1つの分岐のみが実行される。

「前判定反復(while文)」は、箱の左側を二重線とする。

「後判定反復(repeat〜until文)」、「問題向き反復(for文)」は箱の右側を二重線とする。 Cでの後判定反復の実装にはrepeat〜until文の代わりにdo〜while文を用いる。 このとき、条件文が逆(否定)になることに注意する。

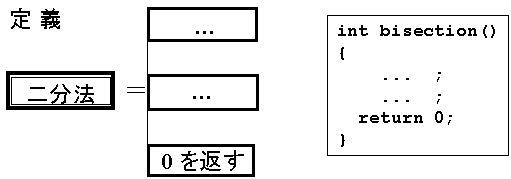
「定義」、「引用(参照)」は箱の内部に手続き名などを書き、両側あるいは境界を二重線とする。 定義は、箱の右側から二重線を横に出して処理ブロックに結ぶ。

引用(参照)は箱の両側または境界が二重線であること以外は処理箱と同様の扱いとなる。

PADのテンプレート

1. ここ(pad.ppt)を右クリックし、 「対象をファイルに保存」で演習1_課題4用のフォルダに保存する。
2. pad.pptを開き、ファイル内のPADをPowerPointの新規スライドに コピー・貼り付けし、グループ解除し、加工する。
3. 加工し終わったらペイントツールを立ち上げ、新規ページを小さめにしておく。
4. 完成したPADをPowerPoint上でドラッグ選択し、コピーする。
5. ペイントツール上で新規ページに貼り付け、画像ファイルとして名前をつけて保存する。

Wordなどで挿入できるファイル形式(jpeg, gif, tiffなど)にしておけば、レポート作成に利用できる。

また、Word上で書いたPADのサンプルも用意した。 次のように、判断（選択）の箱をフローチャートの「記憶データ」で代用している。 (上から処理箱を重ねればもう少し見栄えが良くなるが…。) レポートにはこちらの方法で描いてもよいことにする。

---

【目次】 | 【2.】| 【3.】| 【付録1】 | 【付録2】