プログラミング演習1


― 課題4 数値解析 ―

2. 非線形方程式

2.1 二分法

y ＝ f (x) ＝ x 2 - 2 のグラフにおいて、 x 軸との交点を求めれば 2 の平方根 √2 を求めることができる。

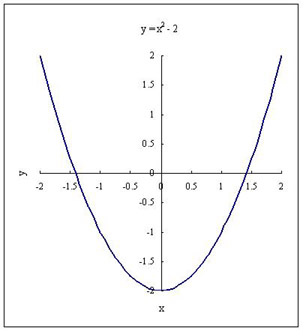
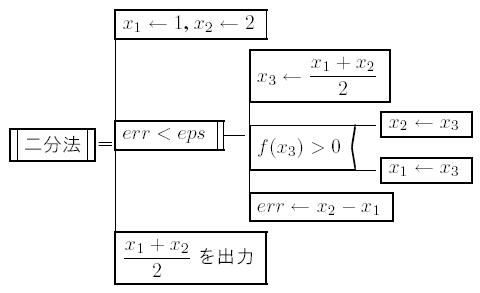
√2 は区間 [1, 2] に含まれているが、この区間を中点 x3 = 1.5 で半分ずつに分け、 交点を含む側を選択すると、新しい区間は[1,1.5]となる。 この操作を繰り返すことによって区間 [x1, x2] を順次狭めていき、 交点の近似値を求める方法を 二分法 という。 交点を含む側の選択法は、x > 0 で y = f (x) が右上がりであることを利用し、 中点での関数値 f (x3) > 0 のときに中点 x3 を 新しい区間の右端とし、そうでないときは x3 を区間の左端とする。

櫻井・熊谷「Pascalで学ぶプログラミング」の例題3.1に記載されている 二分法のPADを以下に示す。

ここに、f (x) = x 2-2 であり、 eps は例えば eps = 1 x 10-6とする。

これをCに移植し、途中経過も出力するように(下線部分を追加)したものを以下に示す。 

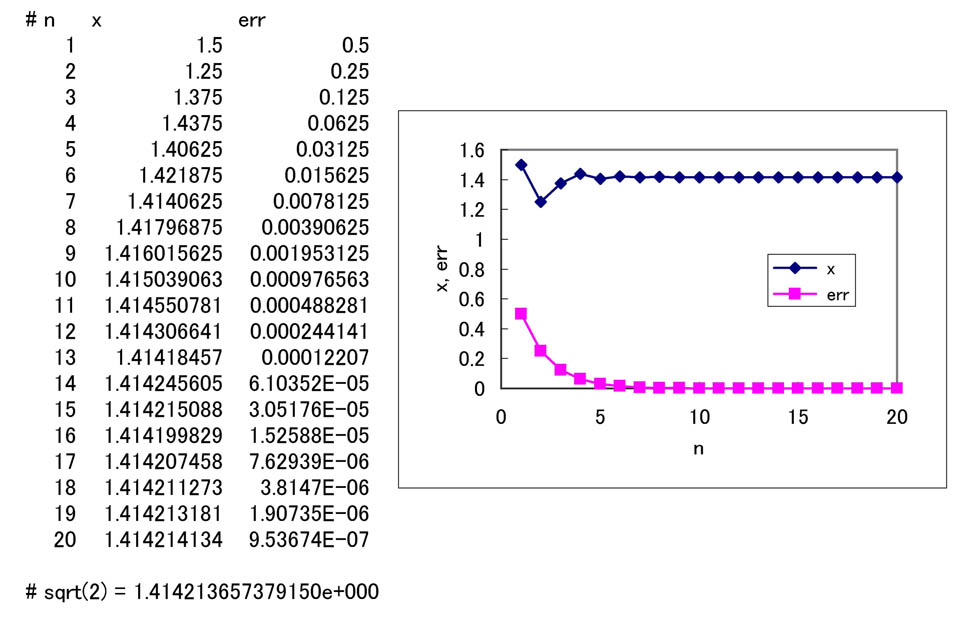
 1: /* bisection.c */
 2: #include <stdio.h>
 3: 
 4: double f(double x);
 5: //  f(x) = x^2 - 2
 6: {
 7:     return x * x - 2.O;
 8: }
 9:
10: main()
11: {
12:     int n = 0;
13:     double x1, x2, x3, err;
14:     double eps = 1.0 e-6;
15:
16:     xl = 1.0;
17:     x2 = 2.0;
18:     printf("# n, x, err\n");
19:     do {
20:         n++;
21:         x3 = (x1 + x2) / 2.0;
22:         if (f(x3) > 0.0) x2 = x3
23:         else             x1 = x3;
24:         err = x2 - x1;
25:         printf("%4d, % .15e, % .15e\n", n, x3, err);
26:     } while (err >= eps);
27: 　　printf("\n# sqrt(2) = % .15e\n"，(x1 + x2) / 2.0);
28:     retrun (O);
29: }
# 上記プログラムにはバグが潜んでいるので注意!

出力結果をcsvファイルに保存し、Excelでグラフに描画したものを示す。

課題4-1

以下の要求を満たす2分法のプログラムを作成せよ。

(1) 上述のプログラムは精度を自由に変えることができない。 また、もう一つの解 -√2 を求めることも出来ない。 そこで、
― 初期区間 [x1, x2] の値と 精度 eps を入力できること
という仕様を追加する。 ただし、x < 0 では関数が右下がりになるので、区間を選択する条件が変わることに注意せよ。 たとえば f (x1)*f (x3) の符号で判断すれば、 余計な場合分けをしなくて済む。 動作テストとして、初期区間[-2, -1], eps = 1.0 e-10 の場合の実行例を報告せよ。 ただし、レポートに添付するデータは最初と最後の数行のみで、途中は省略してよい。

(2) 初期区間を入力するようにしたプログラムでは、 誤差を極端に小さく(たとえば eps = 1 x 10-16 に)した場合に do〜while の反復が止まらなくなる。 また、交点が0かまたは2個以上あるような区間(たとえば[2, 6], [-6, -2]あるいは[-6, 2]) から開始した場合や、 x1, x2 の大きさが x1 > x2 の場合、誤った結果を求めてしまう。 そこで、
(2-1) 反復が止まらない場合はエラーメッセージ "*** 反復回数が100回を超えました。***" を出して、 有限(N=100)回で止まること
(2-2) 入力値が x1 > x2 でも解が求められること
(2-3) 初期区間の数値が異常な場合 (例えばf (x1)とf (x2), f (x3)の符号がすべて同じ場合) は入力し直すこと
という仕様を追加する。 これらの要求を満たしていることを示すため、上記の入力例での対策後の動作を検証し、 出力結果を報告せよ。

作成したプログラムが上記の仕様を満たせなかった場合は、 その旨をレポートで報告すること。

【オプション課題】
(3) さらに余力のある人は、上記の機能を保ったまま、以下の要求を満たしてみよ。
(3-1) 二分法のアルゴリズムの部分(18行目〜26行目)を bisection() と名づけ、 main関数から独立させる。 

double bisection(double x1, double x2, double eps)
{
    …………………………
    二分法のアルゴリズム
    …………………………
    return (x1 + x2) / 2.0;
}
(3-2) 方程式の左辺の関数 f (x) の名前をmain関数側で 自由に指定できるように、bisection の引数に関数ポインタを含めて定義する。 
double bisection(double (*f)(double x), double x1, double x2, double eps)
{
    …………………………
    二分法のアルゴリズム
    …………………………
    return (x1 + x2) / 2.0;
}

【目次】 | 【1.】 | 【2.のつづき】 | 【3.】 | 【付録1】 | 【付録2】