その他の画像処理の補足解説

ぼかし処理（平均値フィルタリング）

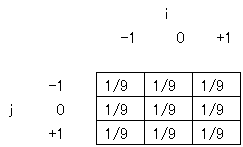
以下は，3×3の移動平均による平滑化を行う際に使用する係数ウィンドウである．平滑化を行うことで，画像にぼけたような効果を与えることができる．

 

原画像中の座標位置（x, y）にある画素値を I（x, y）とし，上記の係数行列 の要素　c(i, j) を用いて i = -1～+1, ｊ = -1～+1について積和演算を行うと，ぼかし処理後の画素値 I'（x, y）が得られる．

I'(x, y) = Σ Σ　I(x+i, y+j) * c(i, j)

これは，画素 I（x, y） とその近傍の画素の平均値を求めることと等しい．

輪郭強調（鮮鋭化フィルタリング）

以下は，輪郭強調のための行列の例である．

 

エッジ検出

以下は，エッジ検出のための行列の例である．

 

縮小

以下の3種の方法について説明する．いずれの方式も，原画像を縦横各1/2に縮小する．（面積は1/4になる．）

(1)サブサンプリング法

原画像の隣接する２×２画素ごとに1画素をサンプリングし，縮小画像の画素とする．

(2)平均化法

原画像の隣接する２×２画素ごとに平均値を求め，これを縮小画像の画素値にする．平均化により発生した小数点以下の数値は，切捨てや四捨五入などにより整数化する．ただし，原画像が画素あたり8ビットで表現されている場合，表現できる値は０～２５５であるので，この範囲を超えないよう注意する． 

(3)平滑化処理後にサブサンプリング

平均値フィルタリングなどを用いて平滑化処理を施してからサブサンプリングを行う方法．折り返し歪を抑制できる．

拡大

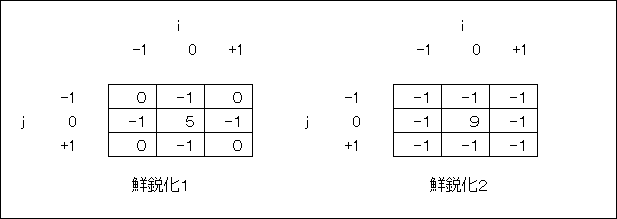
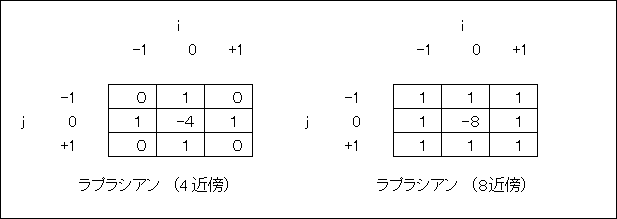
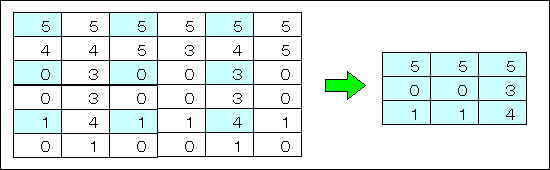
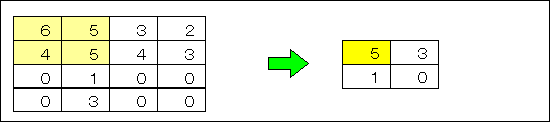
ここでは，線形補間法について説明する．線形補間法では，下図に示すように，原画像上の画素を1画素おき，1ラインおきに配置し，その間の画素を，近傍画素からの線形補間により求めることで，拡大画像を得る．

ｘ = （a+b）/2

y = （a+b+c+d）/4

小数点以下の値の扱いに注意すること．

回転

画像を反時計回りにθ回転させる式は以下のようになる．

X = x cosθ+ｙ sinθ

Y = -x sinθ+ｙ cosθ

ｘ，ｙ　は回転前の座標，Ｘ，Ｙは回転後の座標である．

 

逆変換式は以下のようになる．

ｘ = Ｘ cosθ-Ｙ sinθ

ｙ = Ｘ sinθ+Ｙ cosθ

回転の中心をどうとるか，よく考えて実装すること．