[参考図書:河村哲也著,数値計算入門,サイエンス社,pp.11-20.]
\( x \) に関する方程式を\( f(x) = 0 \) の形に書くことにする。\( f(x) \) が多項式でしかも次数が4以下の場合には、根を求める公式がある。しかし、それ以外の場合には根の存在がわかっていても、特殊な場合を除いて、公式の形では根は表せない。そこで数値的に根を求める必要がある。
その代表的な方法(3.1 二分法と3.2 ニュートン法)を紹介する。これらの方法は、\( f(x) = 0 \) の実根が \( y = f(x) \) と \( x \) 軸の交点であることを利用する。
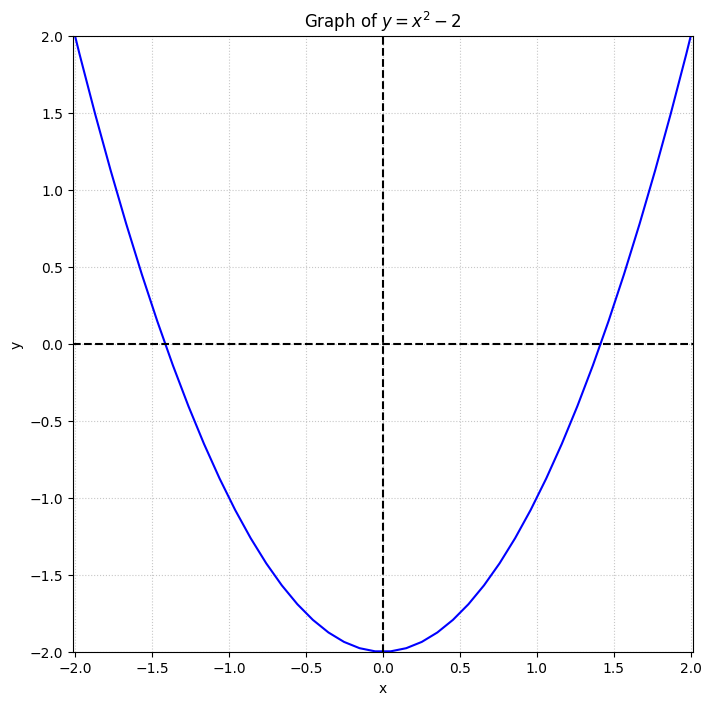
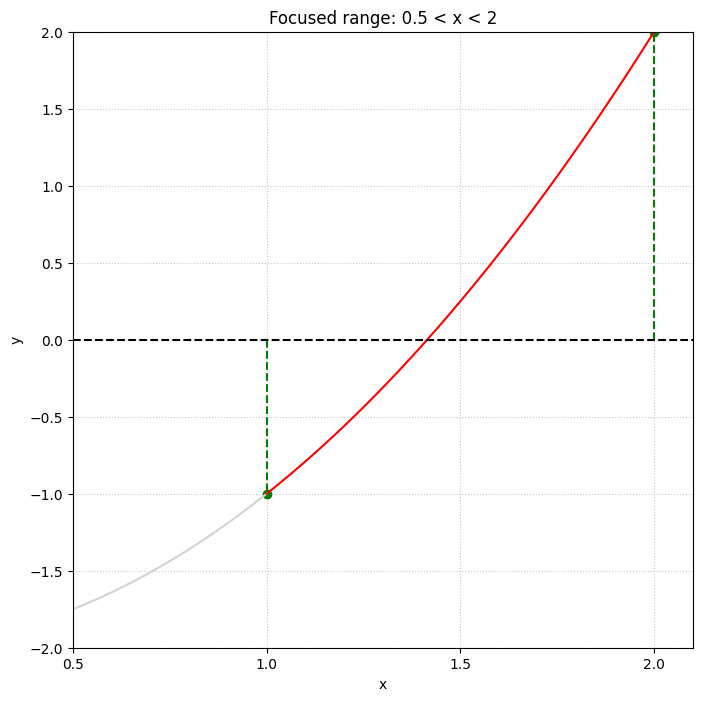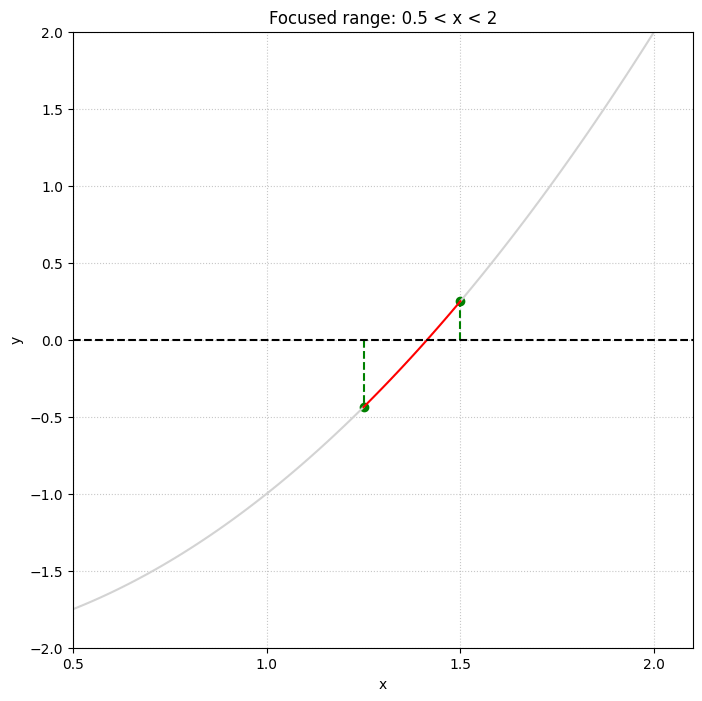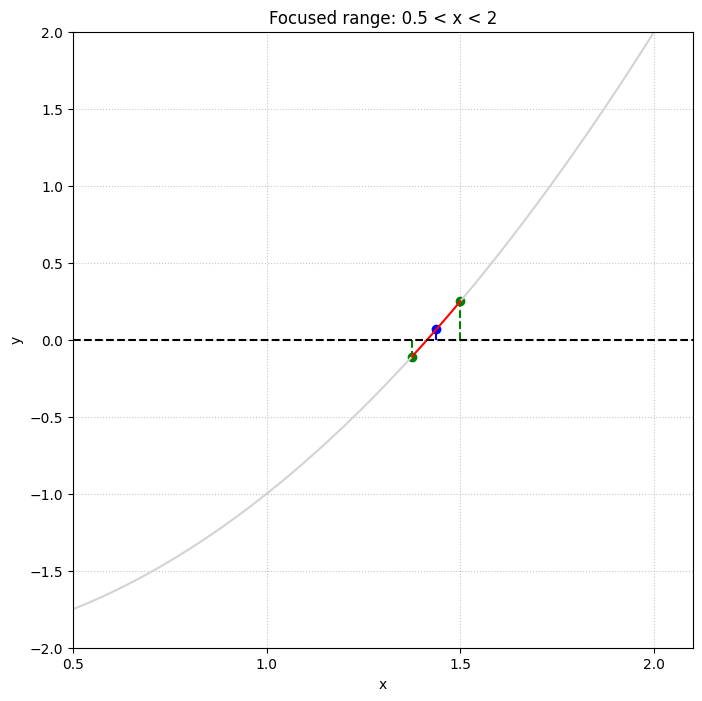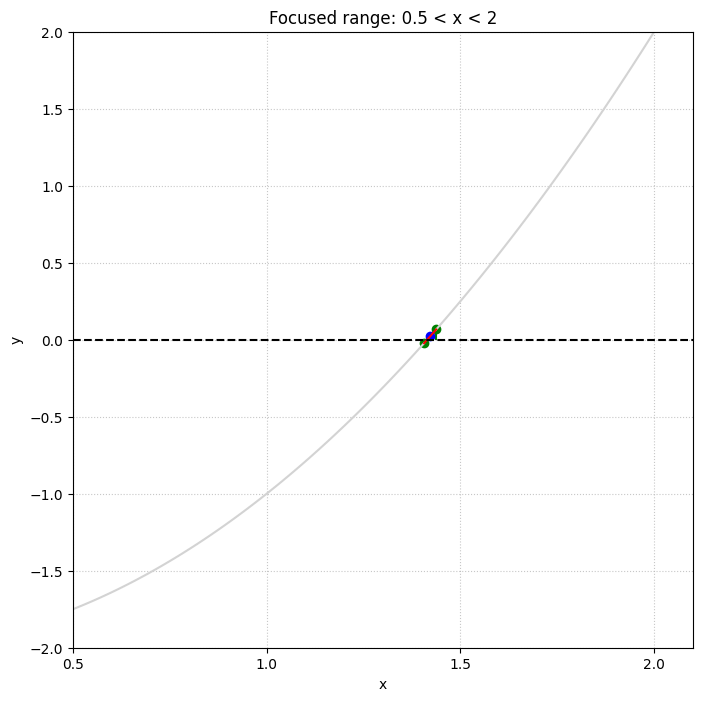
\( y = f(x) = x^2-2\) のグラフにおいて、\( x \) 軸との交点を求めれば \(2\) の平方根 \( \sqrt{2} \) を求めることができる。 \( \sqrt{2} \) は区間 \( [1, 2] \) に含まれているが、この区間を中点 \( x_3 = 1.5\) で半分ずつに分け、交点を含む側を選択すると、新しい区間は\( [1, 1.5] \) となる。この操作を繰り返すことによって区間\( [x_1, x_2] \) を順次狭めていき、交点の近似値を求める方法を二分法という。
交点を含む側の選択法は、\( x\gt 0 \) で \( y = f(x)\) が右上がりであることを利用し、中点での関数値 \( f(x_3) \gt 0\) のときに中点 \( x_3\) を新しい区間の右端とし、そうでないときは \( x_3\) を区間の左端とする。



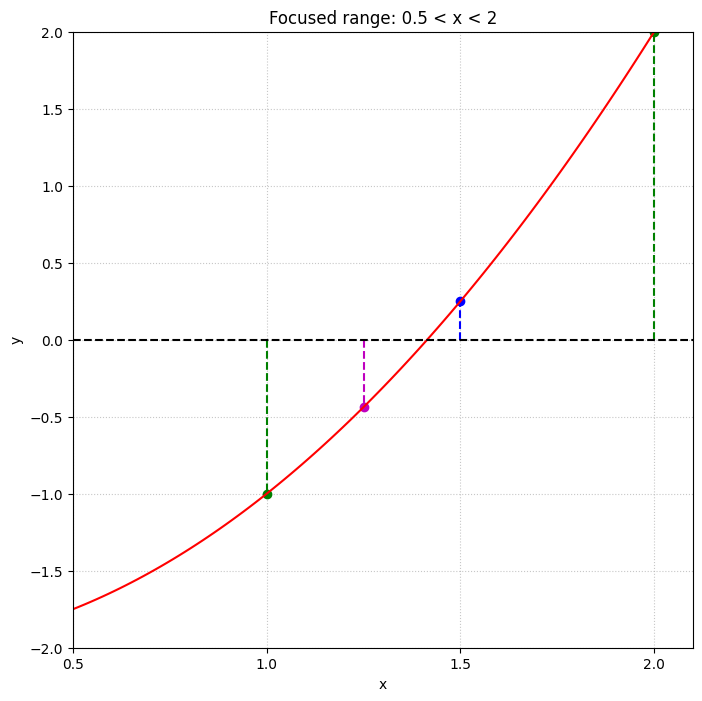
中央と右の図は、左のグラフの\( 0.5\lt x\lt 2\)の範囲を拡大表示したものである。緑の点線がそれぞれ \( x_1\) と \( x_2\) の初期値を示している。最初の反復では \( x_3=(x_1+x_2)/2=1.5\) であるから、\( x_3\) は青色の点線の位置になる。そして、\( f(x_3)\gt0\) であるから、\( x_2\) の値を更新して次の反復を行う。
この処理を記述したコードを以下に示す。ただし、アルゴリズムの核心部分(1)~(10)は穴埋めをして完成させる必要がある。
/*
bisec.c: Bisection Method
*/
#include <stdio.h>
double f(double x)
// f(x) = x^2 - 2
{
return __(1)__;
}
int main(void)
{
int n=0;
double x1, x2, x3, err;
double eps = 1.0e-6;
x1 = __(2)__;
x2 = __(3)__;
printf("Iteration, approx, err\n");
do {
n++;
x3 = __(4)__;
if (__(5)__) __(6)__; // f(x3)の値により、x1またはx2を更新
else __(7)__;
err = __(8)__;
printf("%4d, % .15e, % .15e\n", n, x3, err);
} while (__(9)__); // errが十分小さければ計算終了
fprintf(stderr, "\n sqrt(2) = % .15e\n", __(10)__);
return 0;
}
上記プログラムを完成させて実行してください。
いろいろな条件でプログラムを実行するために、初期区間と精度を入力できるようにしたい。しかし、scanf関数は、“最大文字数が指定できないこと”や“改行コードが空白として扱われてしまう” などの問題を抱えている(例題で学ぶC言語p.121 参照)。そこで、代わりにfgets関数とsscanf関数の組み合わせを使う。通常は以下のように
int main(void)
{
double x1, x2, eps;
…
printf("x1, x2, eps = ");
scanf("%lf%lf%lf", &x1, &x2, &eps);
…
}
int main(void)
{
double x1, x2, eps;
char s[128];
…
printf("x1, x2, eps = ");
fgets(s, 128, stdin);
sscanf(s, "%lf%lf%lf", &x1, &x2, &eps);
…
}
初期値の読み込みができるように二分法のプログラムを変更してください。
[実行結果(例)]
-----------------------
x1, x2, eps = 1 2 1e-2
Iteration, approx, err
1, 1.500000000000000e+00, 5.000000000000000e-01
2, 1.250000000000000e+00, 2.500000000000000e-01
3, 1.375000000000000e+00, 1.250000000000000e-01
4, 1.437500000000000e+00, 6.250000000000000e-02
5, 1.406250000000000e+00, 3.125000000000000e-02
6, 1.421875000000000e+00, 1.562500000000000e-02
7, 1.414062500000000e+00, 7.812500000000000e-03
sqrt(2) = 1.414062500000000e+00
\( x\lt0\) では関数が右下がりになるので、区間を選択する条件が変わる。if 文を用いて条件を切り替える方法もあるが、たとえば \( f(x_1)*f(x_3)\) の符号で判断すれば、余計な場合分けをしなくて済む。
区間を更新する条件式を変更して、負領域の解も求められるようにしてください。初期値を x1 = -2, x2 = -1, eps = 1e-10 として動作を確認しましょう。
[実行結果(例)]
-----------------------
x1, x2, eps = -2 -1 1e-10
Iteration, approx, err
1, -1.500000000000000e+00, 5.000000000000000e-01
2, -1.250000000000000e+00, 2.500000000000000e-01
…
sqrt(2) = -1.414213562326040e+00
精度を入力できるようにしたプログラムでは、誤差を極端に小さくした場合に do~while の反復が止まらなくなる可能性がある。例えば、精度eps=1e-16として実行すると、どうなるだろうか?
無限ループに陥ることを防ぐため、以下の実行例のようにエラーメッセージを表示して有限回(N = 100)で止まるようにプログラムを変更しよう。
[実行結果(例)]
-----------------------
x1, x2, eps = 1 2 1e-16
Iteration, approx, err
1, 1.500000000000000e+00, 5.000000000000000e-01
2, 1.250000000000000e+00, 2.500000000000000e-01
…
100, 1.414213562373095e+00, 2.220446049250313e-16
*** 反復回数が100回を超えました。***
sqrt(2) = 1.414213562373095e+00
初期区間に解が含まれない場合は、誤った解に収束してしまう。例えば、\(x_1\) と \(x_2\) の初期値を逆に入力してみると、errが負の値になりepsよりも小さくなるため、すぐに計算が終了してしまう。あるいは、x1 = 1.5, x2 = 2 のように、解が含まれない初期区間を与えると間違った値に収束する。
[実行結果(例)]
-----------------------
x1, x2, eps = 2 1 1e-6
Iteration, approx, err
1, 1.500000000000000e+00, -5.000000000000000e-01
sqrt(2) = 1.500000000000000e+00
初期値が \(x_1\gt x_2\) の場合でも正しく解が求まるようにしてください。
初期区間において \(f(x)\) が \(x\) 軸にまたがっていないことを調べれば、明らかに解が含まれない場合を除外することができます。具体的には、\(f(x_1), f(x_2), f(x_3) \) の符号がすべて同じ場合に、以下の実行例のようにメッセージを出して終了するようにプログラムを変更してください。
[実行結果(例)]
-----------------------
x1, x2, eps = 2 3 1e-6
*** 初期区間の数値が異常です。***
ここまでの作業で完成したプログラムを使って以下の5通りの条件で実行した結果を示し、正しく値が求まる場合は、それをExcelによりグラフ描画して示すこと。
ヒント: リダイレクト機能を使って出力する場合、初期値の入力を促すメッセージがリダイレクトされるのを防ぐためには、fprintf関数に変更すれば良い。
| \(x_1\) | \(x_2\) | \(eps\) |
|---|---|---|
| 1 | 2 | 1e-6 |
| 2 | 6 | 1e-6 |
| 2 | 1 | 1e-16 |
| -1 | 1 | 1e-6 |
| -1 | -2 | 1e-6 |
ニュートン法は以下の手順で方程式 \( f(x) = 0 \) の解を求める。
ポイントは、関数 \( y = f(x) \) と \( x \) 軸との交点を求める場合に「接線」を利用することである。
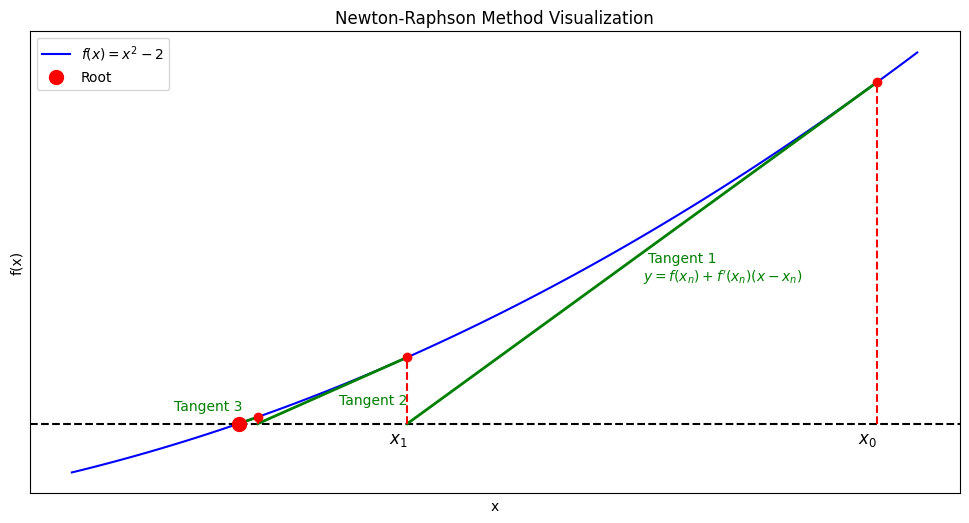
\( (x_0, f(x_0)) \) を通る接線の式 \( y-f(x_0)=f'(x_0)(x-x_0) \) において、\( x \)切片では \( y=0, x=x_1 \) となるので
\( x_1=x_0-f(x_0)/f'(x_0) \) ……… (2.1)
\( f(x)=x^2-a \) のとき、\( f'(x)=2x \) だから
\( x_1=x_0-({x_0}^2-a)/2x_0=(x_0 + a/x_0)/2 \)……… (2.2)
真野芳久「Pascalプログラミングの基礎」サイエンス社 p.41 のプログラムと川上一郎「数値計算」岩波書店 p.180 付録3.1のプログラムを合体してCに移植し、手直ししたものを以下に示す。ただし、アルゴリズムの核心部分(1)~(4)は穴埋めする必要がある。
/*
newton.c: ニュートン法
*/
#include <stdio.h> // printf, fprintf, fgets, sscanf
#include <math.h> // fabs
double a = 0;
int main(void)
{
int n = 0;
double x, x0, err, eps = 1.0e-10;
char s[128];
fprintf(stderr, " a = "); fgets(s, 128, stdin); sscanf(s, "%lf", &a);
while (a <= 0.0) {
fprintf(stderr, "'a' には正の数を入れてください。\n");
fprintf(stderr, " a = "); fgets(s, 128, stdin); sscanf(s, "%lf", &a);
}
x = (a + 1.0) / 2.0;
printf("# n, approx, err\n");
printf("%4d, % .15e\n", n, x);
do {
n++;
x0 = __(1)__;
x = __(2)__;
err = __(3)__;
printf("%4d, % .15e, % .15e\n", n, x, err);
} while (__(4)__);
fprintf(stderr, "\n# sqrt(%e) = % .15e\n", a, x);
return 0;
}
上記のプログラムを完成させよう。a = 2 を入力したときの実行結果は次のようになるはず。
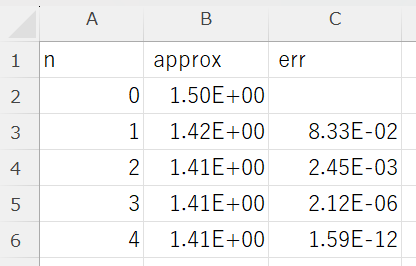
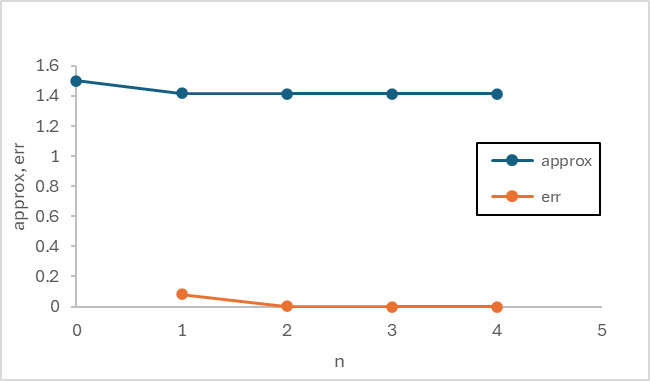
ニュートン法のアルゴリズムの部分(printf("# n, approx, err\n");以降)を newton() と名づけ、 main関数から独立させよう。
具体的には、double newton(double x, double eps)を定義し、main関数からは printf("\n# sqrt(%e) = % .15e\n", a, newton(x, eps));のように利用しよう。
ここまでの作業で完成したプログラムを使ってa = 自分の学籍番号の下3桁, eps = 1e-10 とした場合の実行結果を示し、正しく値が求まる場合は、それをExcelによりグラフ描画して示すこと。
aの値をリダイレクトによって入力する方法を説明してください。実行した様子も示すこと。
関数ポインタについての説明を読み、以下の課題に取り組んでください。
double bisection(double (*f)(double), double x1, double x2, double eps)
{
…………………………
二分法のアルゴリズム
…………………………
return (x1 + x2) / 2.0;
}
double newton(double x, double (*f)(double), double (*df)(double), double eps)
{
…………………………………
ニュートン法のアルゴリズム
…………………………………
return x;
}