プログラミング演習1
― 課題3 数値解析法 ―
3. 非線形方程式
[参考図書:河村哲也著,数値計算入門,サイエンス社,pp.11-20.] x に関する方程式をf(x) = 0 の形に書くことにする。 f(x) が多項式でしかも次数が4以下の場合には、根を求める公式がある。 しかし、それ以外の場合には根の存在がわかっていても、特殊な場合を除いて、 公式の形では根は表せない。そこで数値的に根を求める必要がある。 その代表的な方法(3.1 二分法と3.2 ニュートン法)を紹介する。 これらの方法は、f(x) = 0 の実根がy = f(x) とx軸の交点であることを利用する。
| 3.1 二分法 |
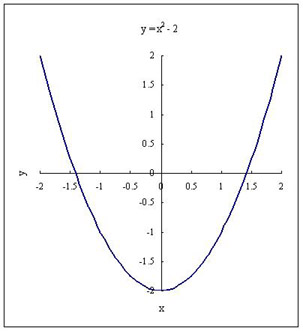
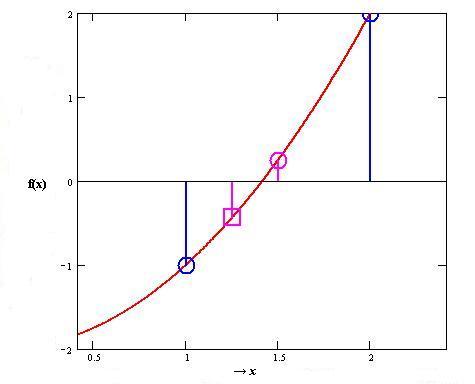
y = f (x) = x 2 - 2 のグラフにおいて、 x 軸との交点を求めれば 2 の平方根 √2 を求めることができる。 √2 は区間 [1, 2] に含まれているが、この区間を中点 x3 = 1.5 で半分ずつに分け、 交点を含む側を選択すると、新しい区間は[1,1.5]となる。 この操作を繰り返すことによって区間 [x1, x2] を順次狭めていき、 交点の近似値を求める方法を 二分法 という。 交点を含む側の選択法は、 x > 0 で y = f (x) が右上がりであることを利用し、 中点での関数値 f (x3) > 0 のときに中点 x3 を 新しい区間の右端とし、そうでないときは x3 を区間の左端とする。
 |
 |
櫻井・熊谷「Pascalで学ぶプログラミング」の例題3.1に記載されている二分法のPAD[2018/6/19更新]を以下に示す。
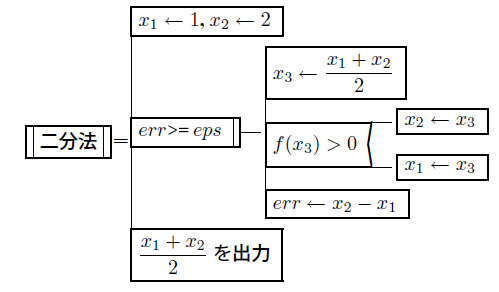
ここで、f (x) = x 2-2 であり、 eps は例えば eps = 1 x 10-6とする。
これをCに移植し、途中経過も出力するように(下線部分を追加)したもの (bisec0.c)を以下に示す。 ただし、アルゴリズムの核心部分(①~⑩)は穴埋めをして完成させる必要がある。
1: /*
2: bisec.c
3: */
4: #include <stdio.h>
5:
6: double f(double x)
7: // f(x) = x^2 - 2
8: {
9: return _____①_____;
10: }
11:
12: int main(void)
13: {
14: int n = 0;
15: double x1, x2, x3, err;
16: double eps = 1.0e-6;
17:
18: x1 = _②_;
19: x2 = _③_;
20: printf("# n, x, err\n");
21: do {
22: n++;
23: x3 = ______④________;
24: if ( ____⑤____ ) ___⑥___;
25: else ___⑦___;
26: err = ___⑧___;
27: printf("%4d, % .15e, % .15e\n", n, x3, err);
28: } while (____⑨_____);
29: printf("\n# sqrt(2) = % .15e\n", _______⑩_______);
30: return 0;
31: }
◎上記プログラムを完成させて実行せよ。
実行結果をグラフに描画したもの(2.1.1 Excelによるグラフ描画の図と同様)を以下に示す。
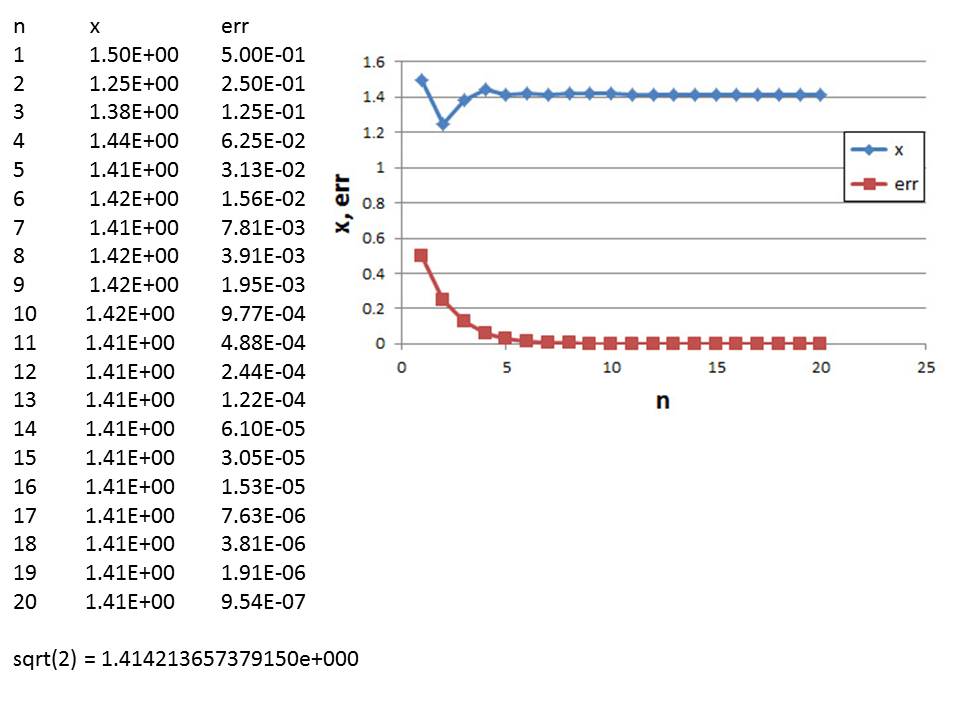
<二分法の特徴(まとめ)> [長所] 上記プログラムは不十分のためレポート課題では仕様の追加を行っているが、 f (x1)*f (x3) <0を満たすようなx1、x3が見つかれば、必ず1つの根が求まること。 [短所] 根を含む区間が1回の手続きで半分に挟まるだけなので根を得るためには 多くの反復が必要であること。また、x1とx3の間に複数の根がある場合に、 どの根が得られるかが不明であること。
| 3.2 ニュートン法 |
ニュートン法は以下の手順で方程式 f (x)=0 の解を求める。 ポイントは、関数 y = f (x) と x軸との交点を求める場合に 「接線」を利用することである。
- 初期値x0を与える。
- その点での関数値f (x0)と 傾きf '(x0)から x 切片x1を推定する。
- x1を新たな初期値x0としてこの操作を反復する。
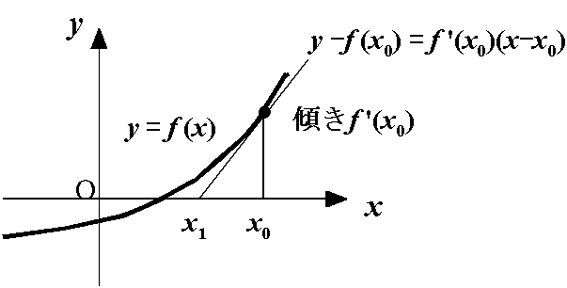
(x0, f (x0))を通る接線の式
y - f (x0) =
f '(x0) (x - x0)
においてx 切片では y = 0, x = x1 となるので
x1 = x0
- f (x0) / f '(x0) ……… (2.1)
f (x) = x2 - a のとき、f '(x) = 2x だから
x1 = x0
- (x02 - a) / 2x0
= (x0 + a / x0) / 2 ……… (2.2)
<ニュートン法の特徴(まとめ)> [長所] 二分法に比べて収束が早いため、解をすぐに得ることができる。 [短所] 必ずしも収束するとは限らない。導関数が必要となる。
真野芳久「Pascalプログラミングの基礎」サイエンス社 p.41 のプログラムと
川上一郎「数値計算」岩波書店 p.180 付録3.1のプログラムを合体してCに移植し、
手直ししたもの(newton0.c)を以下に示す。
ただし、アルゴリズムの核心部分は穴埋め(①~④)する必要がある。
下線部では scanf関数の代わりにfgets関数とsscanf関数
を使って入力する方法を用いた。→[補足説明]を参照
また、リダイレクト出力時にも入力促進メッセージ等がコマンドプロンプトに
出力されるようにfprintf関数を用いて
標準エラー出力(stderr)とした。
1: /*
2: newton.c: ニュートン法
3: */
4: #include <stdio.h> // printf, fgets, sscanf
5: #include <math.h> // fabs
6:
7: int main(void)
8: {
9: int n = 0;
10: double a = 2, x, x0, err, eps = 1.0e-10;
11: char s[128];
12:
13: fprintf(stderr, " a = "); fgets(s, 128, stdin); sscanf(s, "%lf", &a);
14: while (a <= 0.0) {
15: fprintf(stderr, "'a' には正の数を入れてください。\n");
16: fprintf(stderr, " a = "); fgets(s, 128, stdin); sscanf(s, "%lf", &a);
17: }
18:
19: x = (a + 1.0) / 2.0;
20: printf("# n, x, err\n");
21: printf("%4d, % .15e\n", n, x);
22: do {
23: n++;
24: x0 = _①_;
25: x = _______②_______;
26: err = _____③_____;
27: printf("%4d, % .15e, % .15e\n", n, x, err);
28: } while (_____④_____);
29: printf("\n# sqrt(%e) = % .15e\n", a, x);
30: return 0;
31: }
主要部分のアルゴリズムをPAD[2018/6/19更新]で描くと
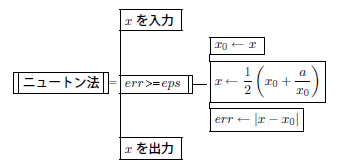
◎上記プログラムを完成させて実行せよ。
" a = 2" を入力したときの実行結果とそのグラフは
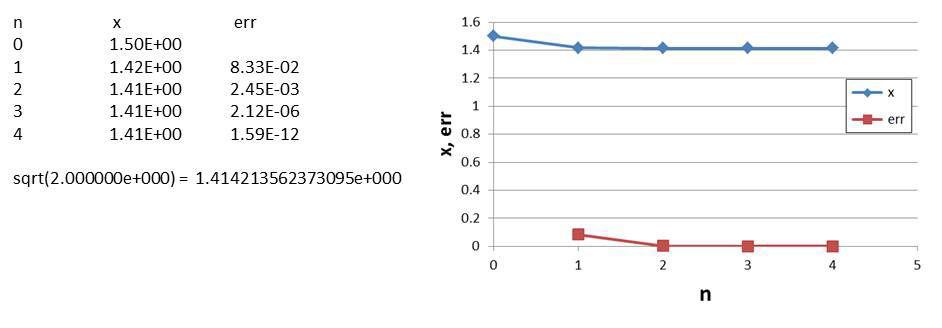
補足説明:scanf関数は使わず、fgets, sscanfのペアを使う
scanf関数は、“最大文字数が指定できないこと”や“改行コードが空白として扱われてしまうこと”
などの問題を抱えている。(例題で学ぶC言語p.121 参照)
そこで、代わりにfgets関数とsscanf関数の組み合わせを使う。通常は
int main(void)
{
double x1, x2, eps;
…
printf(" x1, x2, eps = ");
scanf("%lf%lf%lf", &x1, &x2, &eps);
…
}
と書くところをfgets関数とsscanf関数で置き換えると以下のようになる。
int main(void)
{
double x1, x2, eps;
char s[128];
…
printf(" x1, x2, eps = "); fgets(s, 128, stdin);
sscanf(s, "%lf%lf%lf", &x1, &x2, &eps);
…
}
また、デリミタ(数字の区切り)としてSpace, Tab以外にコンマも許すようにし、
ついでにエラー処理したいときは、以下のように書き換える。
int main(void)
{
double x1, x2, eps;
char s[128];
…
printf(" x1, x2, eps = "); fgets(s, 128, stdin);
if (sscanf(s, "%lf%lf%lf", &x1, &x2, &eps) != 3) // スペース、タブ
if (sscanf(s, "%lf,%lf,%lf", &x1, &x2, &eps) != 3) { // コンマ
printf("*** 入力形式が異常です。 ***\n"); return 1;
}
…
}
【目次】 | 【1.】 | 【2.】