xk+1 = xk + u (xk)
= xk - J (xk)-1 f (xk)
となる。ここに、 J (xk) はヤコビ行列と呼ばれ、
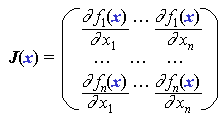
であり、また、 u (x) = - J (x)-1 f (x) である。
| 2.3 二元連立非線形方程式(ニュートン法) |
n 元連立非線形方程式は一般に
f1(x1, x2, ..., xn) = 0,
f2(x1, x2, ..., xn) = 0,
... ... ... ... ...
fn(x1, x2, ..., xn) = 0
と書くことができる。これをベクトル表記すると
f (x)
= 0
となる。
このとき、ニュートン法の計算式は
xk+1
= xk
+ u (xk)
= xk
- J (xk)-1
f (xk)
となる。ここに、
J (xk)
はヤコビ行列と呼ばれ、
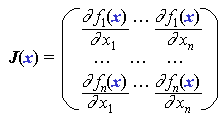
であり、また、
u (x)
= - J (x)-1
f (x)
である。
2変数の場合は、逆行列が簡単に求められるので
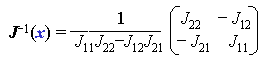
ここに
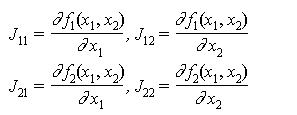
1: /*
2: newton2.c: 2変数のニュートン法
3: x2+y2=1, y=x3 -> (x,y)=(0.826,0.5636),(-0.826,-0.5636)
4: */
5: #include <stdio.h> // printf, fprintf, fgets, sscanf
6: #include <math.h> // hypot(hypotenuse): 直角三角形の斜辺を求める関数
7:
8: double f1(double x, double y)
9: {
10: return x * x + y * y - 1; // f1(x,y) = x2 + y2 - 1
11: }
12: double f2(double x, double y)
13: {
14: return x * x * x - y; // f2(x,y) = x3 - y
15: }
16:
17: double J11(double x, double y)
18: {
19: return 2 * x; // df1(x,y)/dx = 2x
20: }
21: double J12(double x, double y)
22: {
23: return 2 * y; // df1(x,y)/dy = 2y
24: }
25: double J21(double x, double y)
26: {
27: return 3 * x * x; // df2(x,y)/dx = 3x2
28: }
29: double J22(double x, double y)
30: {
31: return -1; // df2(x,y)/dy = -1
32: }
33:
34: int ucalc(double x, double y, double *ux, double *uy)
35: /*
36: u = -J-1(x)*f(x)
37: */
38: {
39: double det;
40:
41: det = J11(x, y) * J22(x, y) - J12(x, y) * J21(x, y);
42: *ux = -1 / det * (J22(x, y) * f1(x, y) - J12(x, y) * f2(x, y));
43: *uy = 1 / det * (J21(x, y) * f1(x, y) - J11(x, y) * f2(x, y));
44: return 0;
45: }
46:
47: int newton2(double *x, double *y, double eps)
48: {
49: int n=0;
50: double x0, y0, ux, uy, err;
51:
52: printf("# n, x, y, err\n");
53: printf("%4d, % .15e, % .15e\n", n, *x, *y);
54: do {
55: n++;
56: x0 = *x; y0 = *y;
57: ucalc(*x, *y, &ux, &uy);
58: *x += ux; *y += uy; // xk+1 = xk + u(xk)
59: err = hypot(*x - x0, *y - y0);
60: printf("%4d, % .15e, % .15e, % .15e\n", n, *x, *y, err);
61: } while (err >= eps);
62: return 0;
63: }
64: // ------------ Main ------------
65: int main(void)
66: {
67: double x=1, y=0.5, eps = 1e-10;
68: char s[128];
69:
70: fprintf(stderr, "# x0 y0 = "); fgets(s, 128, stdin); sscanf(s, "%lf%lf", &x, &y);
71: newton2(&x, &y, eps);
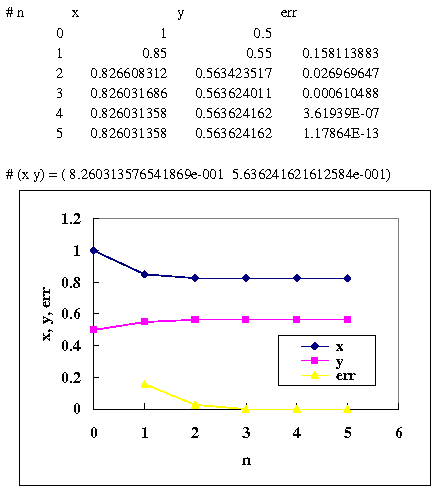
72: printf("\n# (x y) = (% .15e % .15e)\n", x, y);
74: return 0;
75: }
"# x0 y0 = 1 0.5" と入力したときの実行結果とグラフは